Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T12:18:19.552Z Has data issue: false hasContentIssue false
  • English
  • Français

Kähler groups and rigidity phenomena

Published online by Cambridge University Press:  24 October 2008

F. E. A. Johnson  and
E. G. Rees
F. E. A. Johnson
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT
E. G. Rees
Affiliation:
Department of Mathematics, University of Edinburgh, The King's Buildings, Edinburgh EH9 3JZ
Get access Rights & Permissions [Opens in a new window]

Extract

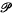The class of fundamental groups of non-singular complex projective varieties is an interesting, but as yet imperfectly understood, class of finitely presented groups. Membership of 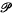is known to be extremely restricted (see [22, 23]). In this paper, we employ geometrical rigidity properties to realize some group extensions as elements of 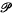as in our previous papers, we find it convenient to work simultaneously with the class ℋ of fundamental groups of compact Kähler manifolds.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 1 , January 1991 , pp. 31 - 44
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Albert, A. A.. Involutorial simple algebras and real Riemann matrices. Ann. of Math. 36 (1935), 886–964.CrossRefGoogle Scholar
[2]Atiyah, M. F.. The signature of fibre bundles. In Collected Papers in Honour of K. Kodaira (Tokyo University Press, 1969). pp. 73–84.Google Scholar
[3]Auslander, L. and Kuranishi, M.. On the holonomy group of locally Euclidean spaces. Ann. of Math. 65 (1957), 411–415.CrossRefGoogle Scholar
[4]Ballmann, W.. Nonpositively curved manifolds of higher rank. Ann. of Math. 122 (1985), 597–609.CrossRefGoogle Scholar
[5]Baily, W. L.. Introductory Lectures on Automorphic Forms (Princeton University Press, 1973).Google Scholar
[6]Bieberbach, L.. Über die Bewegungsgruppen der Euklidischen Raüme I. Math. Ann. 70 (1911), 297–336.CrossRefGoogle Scholar
[7]Bishop, R. L. and O'Neill, B.. Manifolds of negative curvature. Trans. Amer. Math. Soc. 145 (1969), 1–49.CrossRefGoogle Scholar
[8]Borel, A.. Density properties of certain subgroups of semisimple groups. Ann. of Math. 72 (1960), 179–188.CrossRefGoogle Scholar
[9]Borel, A.. On the automorphisms of certain subgroups of semisimple Lie groups. In Algebraic Geometry. Papers Presented at the Bombay Colloquium, 1968 (Oxford University Press, 1969). pp. 43–73.Google Scholar
[10]Charlap, L. S.. Bieberbach Groups and Flat Manifolds (Springer-Verlag, 1986).CrossRefGoogle Scholar
[11]Deligne, P. and Mostow, G. D.. Monodromy of hypergeometric functions and non-lattice integral monodromy. Inst. Hautés Études Sci. Publ. Math. 63 (1986), 5–89.CrossRefGoogle Scholar
[12]Eberlein, P.. Isometry groups of simply connected manifolds of nonpositive curvature II. Acta Math. 149 (1982), 41–69.CrossRefGoogle Scholar
[13]Eells, J. and Sampson, J. H.. Harmonic mappings of Riemannian manifolds. Amer. J. Math. 86 (1964), 109–160.CrossRefGoogle Scholar
[14]Godeaux, L.. Sur une surface algébrique de genre zero et de bigenre deux. Atti Accad. Naz. Lincei 14 (1931), 479–481.Google Scholar
[15]Hartman, P.. On homotopic harmonic maps. Canad. J. Math. 19 (1967), 673–687.CrossRefGoogle Scholar
[16]Helgason, S.. Differential Geometry, Lie Groups and Symmetric Spaces (Academic Press, 1978).Google Scholar
[17]Johnson, F. E. A.. Automorphisms of direct products of groups and their geometric realisations. Math. Ann. 263 (1983), 343–364.CrossRefGoogle Scholar
[18]Johnson, F. E. A.. A class of non-Kählerian manifolds. Math. Proc. Cambridge Philos. Soc. 100 (1986), 519–521.CrossRefGoogle Scholar
[19]Johnson, F. E. A.. On the existence of irreducible discrete subgroups in isotypic Lie groups of classical type. Proc. London Math. Soc. 56 (1988), 51–77.CrossRefGoogle Scholar
[20]Johnson, F. E. A.. Flat algebraic manifolds. In Proceedings of the 1989 Durham Symposium on Low-Dimensional Topology (Cambridge University Press, to appear).Google Scholar
[21]Johnson, F. E. A.. Extending group actions by finite groups. (To appear in Topology.)Google Scholar
[22]Johnson, F. E. A. and Rees, E. G.. On the fundamental group of a complex algebraic manifold. Bull. London Math. Soc. 19 (1987), 463–466.CrossRefGoogle Scholar
[23]Johnson, F. E. A. and Rees, E. G.. On the fundamental group of a complex algebraic manifold II. In Proceedings of Poznan International Conference on Algebraic Topology 1989. (To appear.)Google Scholar
[24]Kerckhoff, S. P.. The Nielsen realisation problem. Ann. of Math. (2) 117 (1983), 235–265.CrossRefGoogle Scholar
[25]Kobayashi, S. and Nomizu, K.. Foundations of Differential Geometry, vol. 2 (Wiley-Interscience, 1969).Google Scholar
[26]Kodaira, K.. On Kähler varieties of restricted type. Ann. of Math. 60 (1954), 28–48.CrossRefGoogle Scholar
[27]Kodaira, K.. A certain type of irregular algebraic surface. Jour. Anal. Math. 19 (1967), 207–215.CrossRefGoogle Scholar
[28]Koebe, P.. Über die Uniformisierung algebraischer Kurven. Math. Ann. 67 (1909), 145–224.CrossRefGoogle Scholar
[29]Lemaire, L.. Harmonic mappings of uniformly bounded dilation. Topology 16 (1977), 199–201.CrossRefGoogle Scholar
[30]Lichnerowicz, A.. Applications harmoniques et variétés Kählériennes. Sympos. Math. 3 (1970), 341–402.Google Scholar
[31]Maclane, S.. Homology (Springer-Verlag, 1967).Google Scholar
[32]Mal'cev, A. I.. On a class of homogeneous spaces. Amer. Math. Soc. Transl. 39 (American Mathematical Society 1951).Google Scholar
[33]Mangler, W.. Die Klassen topologischer Abbildungen einer geschlossenen Fläche auf sich. Math. Z. 44 (1939), 541–554.CrossRefGoogle Scholar
[34]Mostow, G. D.. Strong rigidity of locally symmetric spaces. Annals of Math. Studies no. 78 (Princeton University Press, 1973).Google Scholar
[35]Mostow, G. D. and Siu, Y. T.. A compact Kähler surface of negative curvature not covered by the ball. Ann. of Math. 112 (1980), 321–360.CrossRefGoogle Scholar
[36]Nielsen, J.. Abbildungsklassen endlicher Ordnung. Acta Math. 75 (1943), 23–115.CrossRefGoogle Scholar
[37]Raghunathan, M. S.. Discrete Subgroups of Lie Groups. Ergeb. der Math. no. 68 (Springer-Verlag, 1972).CrossRefGoogle Scholar
[38]Serre, J. P.. Sur la topologie des variétés algébriques en caractéristique p. In Symp. Internacional de Topologia Algebraica, Mexico City (Universidad de Mexico, 1958). pp. 24–53.Google Scholar
[39]Shafarevitch, I. R.. Basic Algebraic Geometry (Springer-Verlag, 1974).CrossRefGoogle Scholar
[40]Siu, Y. T.. The complex analyticity of harmonic maps and the strong rigidity of compact Kähler manifolds. Ann. of Math. (2) 112 (1980), 73–111.CrossRefGoogle Scholar
[41]Webber, D. J. St. H.. On the existence of irreducible discrete subgroups in isotypic Lie groups of exceptional type. Ph.D. Thesis, University of London (1985).Google Scholar
[42]Whitehead, G. W.. Elements of Homotopy Theory. Graduate Texts in Math. no. 61 (Springer-Verlag, 1978).CrossRefGoogle Scholar