Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T14:26:14.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Kadec–Klee properties of vector-valued Hardy spaces

Published online by Cambridge University Press:  24 October 2008

P. N. Dowling  and
C. J. Lennard
P. N. Dowling
Affiliation:
Miami University, Oxford, Ohio 45056, U.S.A.
C. J. Lennard
Affiliation:
University of Pittsburgh, Pittsburgh, PA 15260, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

In 1930, S. Warschawski [19] showed that H1(D), where D is the open unit disc in ℂ, has the following property: Let 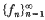be a sequence of functions in H1(D) converging uniformly on compact subsets of D to a function f∈H1(D) and suppose that ‖fn‖1 = |f‖1 = 1 for all n∈ℕ. Then 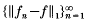converges to zero. From a Banach space standpoint, this result says that H1(D) has the Kadec–Klee property with respect to uniform convergence on compact subsets of D. Warschawski's result was proved independently by Newman [16] in 1963 (see also [13] for another proof) and extended to more general domains by Hoffman [12], Goldstein and Swaminathan [8] and Godefroy [7]. A uniform version of Warschawski's result and its subsequent extensions was recently obtained by Besbes, Dilworth, Dowling and Lennard [2] (see also [1]). We mention here that these results for H1 spaces also hold for the Hp-spaces for 1 < p < ∞ because these spaces are uniformly convex.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 111 , Issue 3 , May 1992 , pp. 535 - 544
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Besbes, M.. Points fixes des contractions definés sur un convexe L 0-fermé de L l. C.R. Acad. Sci. Paris Sér. I Math. 311 (1990), 243–246.Google Scholar
[2]Besbes, M., Dilworth, S., Dowling, P. and Lennard, C.. Convexity properties of Hardy and Lebesgue–Bochner function spaces. Preprint.Google Scholar
[3]Bukhvalov, A. V. and Danilevich, A. A.. Boundary properties of analytic and harmonic functions with values in a Banach space. Math. Notes 31 (1982), 104–110.CrossRefGoogle Scholar
[4]Davis, W. J., Garling, D. J. H. and Tomczak-Jaegermann, N.. The complex convexity of quasi-normed linear spaces. J. Funct. Anal. 55 (1984), 110–150.CrossRefGoogle Scholar
[5]Diestel, J.. Sequences and Series in Banach Spaces. Graduate Texts in Math. no. 92 (Springer-Verlag, 1984).CrossRefGoogle Scholar
[6]Fack, T. and Kosaki, H.. Generalised s-numbers of τ-measurable operators. Pacific J. Math. 123 (1986), 269–300.CrossRefGoogle Scholar
[7]Godefroy, G.. Sous-espaces bien disposés de L 1-applications. Trans. Amer. Math. Soc. 286 (1984), 227–249.Google Scholar
[8]Goldstein, M. and Swaminathan, S.. Pseudo-uniform convexity in Hardy spaces over Riemann surfaces. Math. Ann. 237 (1978), 287–288.CrossRefGoogle Scholar
[9]Haagerup, U.. Lp-spaces associated with an arbitrary von Neumann algebra. Colloq. Internal. CNRS 274 (1977), 175–184.Google Scholar
[10]Haagerup, U. and Pisier, G.. Factorization of analytic functions with values in non-commutative L 1-spaces and applications. Canad. J. Math. 41 (1989), 882–906.CrossRefGoogle Scholar
[11]Hensgen, W.. Hardy–Raüme vektorwertiger Funktionen. Dissertation, Munich (1986).Google Scholar
[12]Hoffman, L. D.. Pseudo-uniform convexity of H1 in several variables. Proc. Amer. Math. Soc. 26 (1970), 609–614.Google Scholar
[13]Kellogg, C. N.. Pseudo-uniform convexity in H l. Proc. Amer. Math. Soc. 23 (1969), 190–192.Google Scholar
[14]Lennard, C. J.. A new convexity property that implies a fixed point property for L 1. Studia Math. 100 (1991), 95–108.CrossRefGoogle Scholar
[15]Nelson, E.. Notes on non-commutative integration. J. Funct. Anal. 15 (1974), 103–116.CrossRefGoogle Scholar
[16]Newman, D. J.. Pseudo-uniform convexity of H l. Proc. Amer. Math. Soc. 14 (1963), 676–679.Google Scholar
[17]Partington, J. R.. On nearly uniformly convex Banach spaces. Math. Proc. Cambridge Philos. Soc. 93 (1983), 127–129.CrossRefGoogle Scholar
[18]Pisier, G.. Factorization of operator valued analytic functions. Preprint.Google Scholar
[19]Warschawski, S.. Über einige Konvergenzsätze aus der Theorie der konformen Abbildungen. Nachr. Akad. Wiss. Göttingen (1930), 344–369.Google Scholar
[20]Xu, Q.. Applications du theoreme de factorisation pour des fonctions a valeurs operateurs. Studia Math. to appear.Google Scholar