Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yang, Zhengguo
Tang, Guoping
and
Liu, Hang
2017.
On the structure of K2(Z[C2×C2]).
Journal of Pure and Applied Algebra,
Vol. 221,
Issue. 4,
p.
773.
Jardine, J. F.
2023.
Victor Percy Snaith, 1944–2021.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 2,
p.
1041.
Zhang, Yakun
2024.
A note on one decomposition of the 2-primary part of
K
2
(ℤ[
C
p
× (
C
2
)
n
])
.
Communications in Algebra,
Vol. 52,
Issue. 6,
p.
2437.


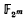 , having 2
, having 2