Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T13:55:36.612Z Has data issue: false hasContentIssue false
  • English
  • Français

Jacobian in genus 2

Published online by Cambridge University Press:  24 October 2008

J. W. S. Cassels
J. W. S. Cassels
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, 16 Mill Lane, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

In [2] the author proposed the study of the geometry and arithmetic of the general curve

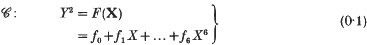
of genus 2 over a general groundfield such as the rationals in order to attack Diophantine problems. He gave the form of the Jacobian, and Flynn[4, 5] determined the group law on it. This paper is preparatory to a planned study of heights under duality. It extends to a general groundfield the description of the Jacobian as the variety of lines on the intersection of two quadric surfaces in P5 given over the complexes in the last chapter of the textbook [7] of Griffiths and Harris. This description is a generalization of that of a curve of genus 1 as the intersection of two quadric surfaces in P3 and is a special case of a more general result [3]: its first appearances seem to be in [12] and [13].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 114 , Issue 1 , July 1993 , pp. 1 - 8
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cassels, J. W. S.. The Mordell–Weil group and curves of genus 2. In Arithmetic and Geometry. Papers dedicated to I. R. Shafarevich on the occasion of his sixtieth birthday. Vol. I, Arithmetic (Birkhäuser, Boston, 1983), pp. 29–60.Google Scholar
[2]Cassels, J. W. S.. Arithmetic of curves of genus 2. In Number Theory and Applications (ed. Mollin, R. A.), NATO ASI Series C, 265 (Kluwer Academic Publishers, 1989), pp. 27–35.Google Scholar
[3]Donagi, B.. Group law on the intersection of two quadrics. Ann. Scuola Norm. Sup. di Pisa (4) 7 (1980), 217–239.Google Scholar
[4]Flynn, E. V.. The jacobian and formal group of a curve of genus 2 over an arbitrary ground field. Math. Proc. Cambridge Philos. Soc. 107 (1990), 425–441.CrossRefGoogle Scholar
[5]Flynn, E. V.. The group law on the jacobian of a curve of genus 2 (to appear in J. reine angew. Math.)Google Scholar
[6]Grant, D.. Formal groups in genus 2. J. reine angew. Math. 411 (1990), 96–121.Google Scholar
[7]Griffiths, P. and Harris, J.. Principles of Algebraic Geometry. (Wiley-Interscience, 1978).Google Scholar
[8]Hodge, W. V. D. and Pedoe, D.. Methods of Algebraic Geometry, vol. II (Cambridge University Press, 1952), pp. 232–234.Google Scholar
[9]Hudson, R. W. H. T.. Kummer's Quartic Surface (Cambridge University Press, 1905; reprinted with commentary by Barth, W., Cambridge University Press, 1990).Google Scholar
[10]Jessop, C. M.. Quartic Surfaces with Singular Points (Cambridge University Press, 1916).Google Scholar
[11]Klein, F.. Zur Theorie der Liniencomplexe des ersten und zweiten Grades. Math. Annalen 2 (1870), 198–226.CrossRefGoogle Scholar
[12]Narasimhan, M. S. and Ramanan, S.. Moduli of vector bundles on a compact Riemann surface. Annals of Math. 89 (1969), 14–51.CrossRefGoogle Scholar
[13]Reid, M. A.. The complete intersection of two or more quadrics. Ph.D. thesis, Cambridge University (1972).Google Scholar