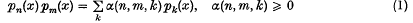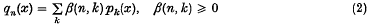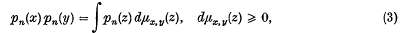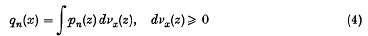Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Askey, Richard
1971.
Orthogonal Expansions with Positive Coefficients. II.
SIAM Journal on Mathematical Analysis,
Vol. 2,
Issue. 3,
p.
340.
Trench, William F.
1973.
Nonnegative and Alternating Expansions of One Set of Orthogonal Polynomials in Terms of Another.
SIAM Journal on Mathematical Analysis,
Vol. 4,
Issue. 1,
p.
111.
Askey, Richard
1974.
Certain Rational Functions Whose Power Series Have Positive Coefficients. II.
SIAM Journal on Mathematical Analysis,
Vol. 5,
Issue. 1,
p.
53.
Zaremba, S. K.
1975.
Some properties of polynomials orthogonal over the set 〈1, 2, ...N〉.
Annali di Matematica Pura ed Applicata,
Vol. 105,
Issue. 1,
p.
333.
Gasper, George
1975.
Positive Integrals of Bessel Functions.
SIAM Journal on Mathematical Analysis,
Vol. 6,
Issue. 5,
p.
868.
Gasper, George
1975.
Theory and Application of Special Functions.
p.
375.
Askey, R.
and
Bingham, N. H.
1976.
Gaussian processes on compact symmetric spaces.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 37,
Issue. 2,
p.
127.
Trench, William F.
1976.
Orthogonal Polynomial Expansions with Nonnegative Coefficients.
SIAM Journal on Mathematical Analysis,
Vol. 7,
Issue. 6,
p.
824.
Askey, Richard
and
Gasper, George
1977.
Convolution structures for Laguerre polynomials.
Journal d'Analyse Mathématique,
Vol. 31,
Issue. 1,
p.
48.
Rahman, Mizan
1978.
A Positive Kernel for Hahn–Eberlein Polynomials.
SIAM Journal on Mathematical Analysis,
Vol. 9,
Issue. 5,
p.
891.
Koornwinder, Tom
and
Sprinkhuizen-Kuyper, Ida
1978.
Generalized Power Series Expansions for a Class of Orthogonal Polynomials in Two Variables.
SIAM Journal on Mathematical Analysis,
Vol. 9,
Issue. 3,
p.
457.
Flensted-Jensen, Mogens
and
Koornwinder, Tom H.
1979.
Jacobi functions: The addition formula and the positivity of the dual convolution structure.
Arkiv för Matematik,
Vol. 17,
Issue. 1-2,
p.
139.
Cazzaniga, Franco
and
Meaney, Christopher
1982.
A local property of absolutely convergent Jacobi polynomial series.
Tohoku Mathematical Journal,
Vol. 34,
Issue. 3,
Wimp, Jet
1983.
Irreducible recurrences and representation theorems for 3F2(1).
Computers & Mathematics with Applications,
Vol. 9,
Issue. 5,
p.
669.
Askey, Richard
and
Wilson, J. A.
1984.
A recurrence relation generalizing those of Apéry.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 36,
Issue. 2,
p.
267.
Nassrallah, B.
and
Rahman, Mizan
1985.
Projection Formulas, a Reproducing Kernel and a Generating Function for q-Wilson Polynomials.
SIAM Journal on Mathematical Analysis,
Vol. 16,
Issue. 1,
p.
186.
Rahman, Mizan
and
Shah, Mihr J.
1985.
An Infinite Series with Products of Jacobi Polynomials and Jacobi Functions of the Second Kind.
SIAM Journal on Mathematical Analysis,
Vol. 16,
Issue. 4,
p.
859.
Lewanowicz, S.
1986.
Properties of the polynomials associated with the Jacobi polynomials.
Mathematics of Computation,
Vol. 47,
Issue. 176,
p.
669.
Gasper, George
1990.
Orthogonal Polynomials.
p.
163.
Lubinsky, Doron S.
and
Totik, Vilmos
1994.
Best Weighted Polynomial Approximation via Jacobi Expansions.
SIAM Journal on Mathematical Analysis,
Vol. 25,
Issue. 2,
p.
555.