1. Let {Vi}i≥0 be a weakly (hence also strongly) continuous semigroup of (linear) contraction operators on a Hilbert space H, i.e. |Vt| ≤ 1 ( t ≥ 0). Let Z and W denote the corresponding infinitesimal generator and cogenerator, i.e.

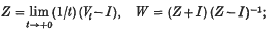
Z is in general non-bounded, but closed and densely defined, and W is a contraction operator (everywhere defined in H), such that 1 is not a proper value of W. Conversely, every contraction operator W not having the proper value 1 is the infinitesimal cogenerator of exactly one semigroup {Vi} of the above type; one has namely

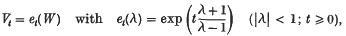
in the sense of the functional calculus for contraction operators (4).