Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T14:43:19.901Z Has data issue: false hasContentIssue false
  • English
  • Français

Involutory *-antiautomorphisms on On

Published online by Cambridge University Press:  24 October 2008

P. J. Stacey
P. J. Stacey
Affiliation:
Department of Mathematics, La Trobe University, Bundoora, 3083, Victoria, Australia
Get access Rights & Permissions [Opens in a new window]

Extract

Let nℕ{1} and let S1, , Sn be isometries on an infinite-dimensional Hilbert space such that 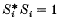for each i and 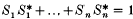. It was shown in 1 that the C*-algebra On generated by S1, , Sn is an infinite simple C*-algebra which is, up to isomorphism, independent of the choice of isometries satisfying the given relations. Ifis a unital *-endomorphism of On then, as shown in 2, 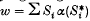is a unitary determiningby the equations (Si) = w*Si and each unitary arises in this way.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 111 , Issue 2 , March 1992 , pp. 319 - 323
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1Cuntz, J.. Simple C*-algebras generated by isometries. Comm. Math. Phys. 57 (1977), 173185.CrossRefGoogle Scholar
2Cuntz, J.. Automorphisms of certain simple C*-algebras. In Quantum. Fields-Algebras Processes (ed. Streit, L.) (Springer-Verlag, 1980), pp. 187196.CrossRefGoogle Scholar
3Cuntz, J.. The structure of addition and multiplication in simple C*-algebras. Math. Scand. 40 (1977), 215233.CrossRefGoogle Scholar
4Cuntz, J.. K-Theory for certain C*-algebras. Ann. of Math. (2) 113 (1981), 181197.CrossRefGoogle Scholar
5Cuntz, J.. K-Theory and C*-algebras. In Proceedings of Conference on K-Theory (Bielefeld, 1982), Lecture Notes in Math. vol. 1046 (Springer-Verlag, 1984), pp. 5579.Google Scholar
6Evans, D. E.. On On. Publ. Res. Inst. Math. Sci. 16 (1980), 915927.CrossRefGoogle Scholar
7Gsemyr, J.. Antiautomorphisms of operator algebras. Preprint (1987).Google Scholar
8Karoubi, M.. K-Theory: An Introduction (Springer-Verlag, 1978).CrossRefGoogle Scholar
9Stacey, P. J.. Stability of involutory *-antiautomorphisms in UHF algebras. J. Operator Theory 24 (1990), 5774.Google Scholar
10Strmer, E.. Conjugacy of involutive antiautomorphisms of von Neumann algebras. J. Fund. Anal. 66 (1986), 5466.CrossRefGoogle Scholar