One of the most celebrated theorems of mathematical analysis is the intermediate value theorem of Bolzano which, in a simple case, states that a real-valued continuous map f of a closed interval [a, b], such that f(a) and f(b) have different signs, has a zero in (a, b). Recently, Shih in [5] observed that without loss of generality we may suppose that a 7 < 0 < b and f(a) < 0 < f(b) and, consequently, the condition f(a).f(b) < 0 becomes x.f(x) > 0 for x∈∂Ω where ∂Ω denotes the boundary of the interval Ω = (a, b); then the conclusion is that f has at least one zero in ω. It is a remarkable fact that Shih extends this form of Boizano's theorem to analytic maps in ℂ [5] and, subsequently, in ℂn [6]. He proved that if Ω is a bounded domain in ℂn containing the origin, 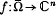is continuous in 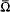and analytic in Ω and Re 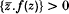for z∈∂Ω, then f has exactly one zero in Ω. In this paper we extend Shih's result to Banach spaces.