Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-29T18:23:21.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Integration of certain products associated with a generalized Meijer function

Published online by Cambridge University Press:  24 October 2008

H. M. Srivastava  and
C. M. Joshi
H. M. Srivastava
Affiliation:
Department of Mathematics, Jodhpur University, India
C. M. Joshi
Affiliation:
Department of Mathematics, Jodhpur University, India
Get access Rights & Permissions [Opens in a new window]

Abstract

In an attempt to give extensions of certain results in the theory of Mac-Robert's E-function and Meijer's (G-function, the integrals

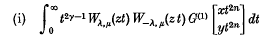
and

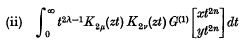
are evaluated, for positive integral values of n, in terms of Agarwal's 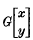and their numerous interesting particular cases are deduced. The scope of a further generalization of (i) and (ii), with the aid of the Mellin inversion formula, is also discussed.

It is observed that the integral (ii) provides an elegant generalization of some of the recent results of Srivastava which, in turn, incorporate a well-known formula due to Slater.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 65 , Issue 2 , March 1969 , pp. 471 - 477
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Agarwal, R. P.An extension of Meijer's (G-function. Proc. Nat. Inst. Sci. India Part A 31 (1965), 536–546.Google Scholar
(2)Bromwich, T. J. I'a.Theory of infinite series (Macmillan; London, 1926).Google Scholar
(3)Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.Higher transcendental functions, vol. i (McGraw-Hill; New York, 1953).Google Scholar
(4)Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.Tables of integral transforms, vol. i (McGraw-Hill; New York, 1954).Google Scholar
(5)Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.Tables of integral transforms, vol. ii (McGraw-Hill; New York, 1954).Google Scholar
(6)MacRobert, T. M.Functions of a complex variable (Macmillan; London, 1954).Google Scholar
(7)Meijer, C. S.On the G-function, i–viii. Nederl. Akad. Wetensch. Proc. Ser. A 49 (1946), 227–237, 344–356, 457–469, 632–641, 765–772, 936–943, 1063–1072, 1165–1175.Google Scholar
(8)Rathie, C. B.Integrals involving E-functions. Proc. Glasgow Math. Assoc. 4 (1960), 186–187.CrossRefGoogle Scholar
(9)Slater, L. J.Confluent hypergeometric functions (Cambridge, 1960).Google Scholar
(10)Srivastava, H. M.The integration of generalized hypergeometric functions. Proc. Cambridge Philos. Soc. 62 (1966), 761–764.CrossRefGoogle Scholar
(11)Srivastava, H. M. and Singhal, J. P.Certain integrals involving Meijer's (G-function of two variables. Proc. Nat. Inst. Sci. India Part A 33 (1967).Google Scholar
(12)Verma, R. U.Integrals involving Meijer's G-functions. Ganita. 16 (1965), 65–68.Google Scholar