Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T13:11:58.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrals with a large parameter: Hilbert transforms

Published online by Cambridge University Press:  24 October 2008

F. Ursell
F. Ursell
Affiliation:
Department of Mathematics, University of ManchesterM13 9PL
Get access Rights & Permissions [Opens in a new window]

Abstract

A simple and elegant method of treating one-sided Hilbert transforms

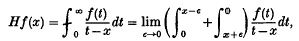
has recently been described by Wong (7). This method immediately gives the form of the expansion but some of the coefficients in the expansion are in an inconvenient form for either analytical or numerical calculation. In the present paper it is shown that these coefficients can be readily determined when the Mellin transform of f(t) is known. The case 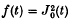is treated as an example.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 93 , Issue 1 , January 1983 , pp. 141 - 149
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bleistein, N. and Handelsman, R. A.Asymptotic expansions of integrals (New York, Holt, Rinehart and Winston, 1975).Google Scholar
(2)Hulme, A.The potential of a horizontal ring of wave sources in a fluid with a free surface. Proc. Roy. Soc. A 375 (1981), 295–305.Google Scholar
(3)Lauwerier, H. A.Asymptotic analysis. Math. Centre Tract no. 54 (Amsterdam, 1974).Google Scholar
(4)Luke, Y. L.SIAM Review 10 (1968), 229–232.CrossRefGoogle Scholar
(5)Watson, G. N.Bessel functions, 2nd ed. (Cambridge, 1944).Google Scholar
(6)Wong, R.Explicit error terms for asymptotic expansions of Mellin convolutions. Jl. Math. Anal. and Applicns. 72 (1979), 740–756.Google Scholar
(7)Wong, R.Asymptotic expansion of the Hilbert transform. SIAM Jl. Math. Anal. 11 (1980), 92–99.CrossRefGoogle Scholar