Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T14:01:56.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrals developable about a singular point of a Hamiltonian system of differential equations. Part II

Published online by Cambridge University Press:  24 October 2008

T. M. Cherry
T. M. Cherry
Affiliation:
Trinity College.
Get access Rights & Permissions [Opens in a new window]

Extract

This paper completes an investigation, of which the first part has already been published, into the integrals of a Hamiltonian system which are formally developable about a singular point of the system. Let

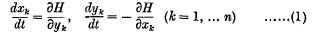
be a system of differential equations of which the origin is a singular point of the first type, i.e. a point at which H is developable in a convergent Taylor series, but at which its first derivatives all vanish. We suppose that H does not involve t, and we consider only integrals not involving t. Let the exponents of this singular point be ± λ1, ± λ2,…±λn. In Part I, I considered the case in which the constants λ1,…λn are connected by no relation of commensurability, i.e. a relation of the form

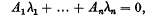
where A1…An are integers (positive, negative or zero) not all zero, and showed that the equations (1) possess n, and only n, integrals not involving t which are formally developable as power series in the xk, yk. In this paper I consider the case in which λ1 … λn are connected by one or more relations of commensur-ability. Suppose that there are p, and only p, such relations linearly independent (p > 0): it will be shown that the equations (1) possess (n − p) independent integrals not involving t, formally developable about the origin and independent of H.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 4 , March 1925 , pp. 510 - 533
Copyright
Copyright © Cambridge Philosophical Society 1925

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Proc. Comb. Phil. Soc. 22, 325 (1924)CrossRefGoogle Scholar: “On integrals developable about a singular point of a Hamiltonian system of differential equations.” This paper will be referred to as Part I.

† So called to distinguish it from a point (singular point of the second type) at which H is not developable.

* In fact, from (12), no term α1a1β1b 1… αnanβnb n for which a 2 = b 2 = 0 is of a type which can occur in [β2, α 3], for this Lagrange bracket has α2 as a factor.

* It must be remembered that these equations do not give the dependence of αk, βk upon t, the equations which do this being since the αk, βk are constants of integration.

* It arises out of their Hamiltonian form; for equations there is no integral developable about a singular point unless some restriction is placed upon the form of x 1, … xn.

* I.e. necessary when λ1, … λn are connected by relations of commensurability; when there are no such relations it is unnecessary, as shown in Part I, § 3.

* Whittaker, (Proc. Boy. Soc. Edin. 37, 95)Google Scholar uses this principle in a problem very similar to the present one, but does not give a general proof that by its application all the critical terms can be annulled.

* From an integral we may derive by combination with H the integral Z – cH 2, which is of the same form as Z with c = 0.

* Since the product χα χβ is critical we have Dαβ = 0, i.e. Dα + Dβ = 0.

* Compare § 2 (ii) above.

* The argument which follows is clearly of a general type.

* Since α2β1 = α1β1.α2β2/α1β2, the fifth series is a function of the first, second and fourth.