Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Graham, R. L.
1983.
Mathematical Programming The State of the Art.
p.
115.
1992.
Convex Functions, Partial Orderings, and Statistical Applications.
Vol. 187,
Issue. ,
p.
419.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1993.
Classical and New Inequalities in Analysis.
p.
239.
Rostamian Delavar, Mohsen
2023.
On Fejér’s inequality: generalizations and applications.
Journal of Inequalities and Applications,
Vol. 2023,
Issue. 1,


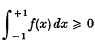 new integral inequalities. They generalize classical results. The proofs are short and simple being based on sequences.
new integral inequalities. They generalize classical results. The proofs are short and simple being based on sequences.