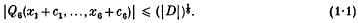Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-20T14:37:25.286Z Has data issue: false hasContentIssue false
  • English
  • Français

Inhomogeneous minimum of indefinite quadratic forms in six variables: A conjecture of Watson

Published online by Cambridge University Press:  24 October 2008

Madhu Raka
Madhu Raka
Affiliation:
Panjab University, Chandigarh-160014, India
Get access Rights & Permissions [Opens in a new window]

Extract

The famous conjecture of Watson(11) on the minima of indefinite quadratic forms in n variables has been proved for n ≤ 5, n ≥ 21 and for signatures 0 and ± 1. For the details and history of the conjecture the reader is referred to the author's paper(8). In the succeeding paper (9), we prove Watson's conjecture for signature ± 2 and ± 3 and for all n. Thus only one case for n = 6 (i.e. forms of type (1, 5) or (5, 1)) remains to he proved which we do here; thereby completing the case n = 6. This result is also used in (9) for proving the conjecture for all quadratic forms of signature ± 4. More precisely, here we prove:

Theorem 1. Let Q6(x1, …, x6) be a real indefinite quadratic form in six variables of determinant D ( < 0) and of type (5, 1) or (1, 5). Then given any real numbers ci, 1 ≤ i ≤ 6, there exist integers x1,…, x6such that

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 94 , Issue 1 , July 1983 , pp. 1 - 8
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bambah, R. P., Dumir, V. C. and Hans-Gill, R. J.On a conjecture of Jackson on non-homogeneous quadratic forms. J. Number Theory (accepted).Google Scholar
(2)Davenport, H.Non-homogeneous ternary quadratic forms. Acta Math. 80 (1948), 65–95.CrossRefGoogle Scholar
(3)Dumir, V. C.Asymmetric inequalities for non-homogeneous ternary quadratic forms. Proc. Cambridge Philos. Soc. 63 (1967), 291–303.CrossRefGoogle Scholar
(4)Hans-Gill, R. J. and Madhu, Raka. Some inequalities for nonhomogeneous quadratic forms. Indian J. pure appl. Math. 11 (1) (1980), 60–74.Google Scholar
(5)Jackson, T. H.Small positive values of indefinite quadratic forms. J. Lond. Math. Soc. (2), 1 (1969), 643–659.CrossRefGoogle Scholar
(6)Jackson, T. H.Gaps between the values of quadratic polynomials. J. Lond. Math. Soc. (2), 3 (1971), 47–58.CrossRefGoogle Scholar
(7)Jackson, T. H.One sided inequalities for quaternary forms. Proc. Lond. Math. Soc. (3), 23 (1971), 267–82.CrossRefGoogle Scholar
(8)Madhu, Raka. The inhomogeneous minimum of quadratic forms of signature ± 1. Math. Proc. Cambridge Philos. Soc. 89 (1981), 225–235.Google Scholar
(9)Madhu, Raka. On a conjecture of Watson. Math. Proc. Cambridge Philos. Soc. 94 (1983), 9–22.Google Scholar
(10)Watson, G. L.Indefinite quadratic polynomials. Mathematika 7 (1960), 141–144.CrossRefGoogle Scholar
(11)Watson, G. L.Indefinite quadratic forms in many variables: The inhomogeneous minimum and a generalization. Proc. Lond. Math. Soc. (3), 12 (1962), 564–576.CrossRefGoogle Scholar