Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1979.
Inequalities - Theory of Majorization and Its Applications.
Vol. 143,
Issue. ,
p.
531.
Kubo, Fumio
and
Ando, Tsuyoshi
1980.
Means of positive linear operators.
Mathematische Annalen,
Vol. 246,
Issue. 3,
p.
205.
Trapp, George E.
1984.
Hermitian semidefinite matrix means and related matrix inequalities—an introduction.
Linear and Multilinear Algebra,
Vol. 16,
Issue. 1-4,
p.
113.
Anderson, W.N.
Morley, T.D.
and
Trapp, G.E.
1984.
Symmetric function means of positive operators.
Linear Algebra and its Applications,
Vol. 60,
Issue. ,
p.
129.
Anderson, Jr., William N.
and
Trapp, George E.
1986.
Inverse Problems for Means of Matrices.
SIAM Journal on Algebraic Discrete Methods,
Vol. 7,
Issue. 2,
p.
188.
Nishii, Ryuei
1988.
Identities and inequalities for the expected values of random matrices and loewner's theory.
Communications in Statistics - Theory and Methods,
Vol. 17,
Issue. 6,
p.
2021.
Kwong, Man Kam
1989.
Some results on matrix monotone functions.
Linear Algebra and its Applications,
Vol. 118,
Issue. ,
p.
129.
Ando, T.
1994.
Majorizations and inequalities in matrix theory.
Linear Algebra and its Applications,
Vol. 199,
Issue. ,
p.
17.
Gustafson, Karl E.
and
Rao, Duggirala K. M.
1997.
Numerical Range.
p.
27.
Pečarić, J.
and
Mond, B.
1997.
General Inequalities 7.
p.
77.
Walsh, Cormac
and
Gunawardena, Jeremy
2001.
Iterates of Maps Which are Non-Expansive in Hilbert's Metric.
IFAC Proceedings Volumes,
Vol. 34,
Issue. 13,
p.
879.
Friedland, Shmuel
and
Porta, Gaspar
2004.
The limit of the product of the parameterized exponentials of two operators.
Journal of Functional Analysis,
Vol. 210,
Issue. 2,
p.
436.
Ertin, E.
Moses, R.L.
and
Potter, L.C.
2004.
Network parameter estimation with detection failures.
Vol. 2,
Issue. ,
p.
ii.
Holbrook, John
and
Bhatia, Rajendra
2006.
Noncommutative geometric means.
The Mathematical Intelligencer,
Vol. 28,
Issue. 1,
p.
32.
Otte, Peter
2010.
Boundedness properties of fermionic operators.
Journal of Mathematical Physics,
Vol. 51,
Issue. 8,
Nordström, Kenneth
2011.
Convexity of the inverse and Moore–Penrose inverse.
Linear Algebra and its Applications,
Vol. 434,
Issue. 6,
p.
1489.
Bhatia, Rajendra
and
Grover, Priyanka
2012.
Norm inequalities related to the matrix geometric mean.
Linear Algebra and its Applications,
Vol. 437,
Issue. 2,
p.
726.
Audenaert, Koenraad M.R.
2012.
Trace inequalities for completely monotone functions and Bernstein functions.
Linear Algebra and its Applications,
Vol. 437,
Issue. 2,
p.
601.
Bhatia, Rajendra
2013.
Matrix Information Geometry.
p.
35.
Audenaert, Koenraad M.R.
2013.
In-betweenness, a geometrical monotonicity property for operator means.
Linear Algebra and its Applications,
Vol. 438,
Issue. 4,
p.
1769.
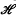 is through the concept of a positive operator. A bounded self-adjoint operator A denned on
is through the concept of a positive operator. A bounded self-adjoint operator A denned on 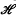 is called positive – and one writes A ≥ 0 - if the inner product (ψ, Aψ) ≥ 0 for every ψ ∈
is called positive – and one writes A ≥ 0 - if the inner product (ψ, Aψ) ≥ 0 for every ψ ∈ 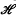 . If, in addition, (ψ, Aψ) = 0 only if ψ = 0, then A is called positive-definite and one writes A > 0. Further, if there exists a real number γ > 0 such that A — γI ≥ 0, I being the unit operator, then A is called strictly positive (in symbols, A ≫ 0). In a finite dimensional space, a positive-definite operator is also strictly positive.
. If, in addition, (ψ, Aψ) = 0 only if ψ = 0, then A is called positive-definite and one writes A > 0. Further, if there exists a real number γ > 0 such that A — γI ≥ 0, I being the unit operator, then A is called strictly positive (in symbols, A ≫ 0). In a finite dimensional space, a positive-definite operator is also strictly positive.

