Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T14:36:52.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Indefinite binary forms representing the same numbers

Published online by Cambridge University Press:  24 October 2008

Li Delang
Li Delang
Affiliation:
Sichuan University, Chengdu, China
Get access Rights & Permissions [Opens in a new window]

Extract

It is an old problem whether two binary quadratic forms representing the same numbers are equivalent. Legendre asserted without proof that two positive definite forms representing the same numbers are equivalent. In 1895, Bauer(1) proved Legendre's assertion for primitive forms with the same discriminant. In 1938 Delone (2) proved that two positive definite binary forms with real coefficients are equivalent if they represent the same numbers, with the sole exception of the pair equivalent to

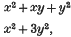
and their scalings. Watson (3) rediscovered this result in 1979 and asked the same question for indefinite binary forms.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 92 , Issue 1 , July 1982 , pp. 29 - 33
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bauer, M. B.Math. és Termés Ertesitö 13 (1895), 316–322.Google Scholar
(2)Delone, B. N.Geometry of positive quadratic forms addendum. Uspehi Mat. Nauk 4 (1938).Google Scholar
(3)Watson, G. L.Determination of a binary quadratic form by its values at integer points. Mathematika 26 (1979), 72–75, andCrossRefGoogle Scholar
Watson, G. L.Determination of a binary quadratic form by its values at integer points. Mathematika 27 (1980), 188.CrossRefGoogle Scholar
(4)Weber, H.Über Zahlen gruppen in algebraischen Zahlkorpern. Mathematische Annalen I, 48 (1897), 433–473;CrossRefGoogle Scholar
Weber, H.Über Zahlen gruppen in algebraischen Zahlkorpern. Mathematische Annalen I, II, 49 (1897), 83–100;CrossRefGoogle Scholar
Weber, H.Über Zahlen gruppen in algebraischen Zahlkorpern. Mathematische Annalen I, III, 50 (1898), 1–26.CrossRefGoogle Scholar