Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T09:37:48.242Z Has data issue: false hasContentIssue false
  • English
  • Français

The Hopf invariant and homotopy groups of spheres

Published online by Cambridge University Press:  24 October 2008

P. J. Hilton
P. J. Hilton
Affiliation:
Victoria UniversityManchester
Get access Rights & Permissions [Opens in a new window]

Extract

In (5), Whitehead introduced a generalization of the Hopfinvariant in the form of a homomorphism H: πr(Sn) → πr(S2n−1), valid† if r < 3n − 3. In (2), the author extended Whitehead's definition to cover the cases r ≤ 4n − 4; r = 5, n = 2; r = 13, n = 4. He also defined, without restriction, a homomorphism

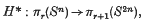
which was related to H, whenever H was defined, by the equation H* = FH, F being the Freudenthal suspension

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 48 , Issue 4 , October 1952 , pp. 547 - 554
Copyright
Copyright © Cambridge Philosophical Society 1952

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Blakers, A. L. and Massey, W. S.The homotopy groups of a triad, I. Ann. Math., Princeton (2), 53 (1951), 161–205.CrossRefGoogle Scholar
(2)Hilton, P. J.Suspension theorems and the generalized Hopf invariant. Proc. Lond. math. Soc. (3), 1 (1951), 462–93.CrossRefGoogle Scholar
(3)Rohlin, V. A.On an application of the (n + 3)-sphere in the n-sphere. C.R. Acad. Sci. U.R.S.S. (Doklady Akad. Nauk. S.S.S.R.), 80 (1951), 541–3 (Russian).Google Scholar
(4)Serre, J. P.Homologie singulière des espaces fibrés. Ann. Math., Princeton (2), 54 (1951), 425–505.CrossRefGoogle Scholar
(5)Whitehead, G. W.Generalization of the Hopf invariant. Ann. Math., Princeton (2), 5 (1950), 192–237.CrossRefGoogle Scholar
(6)Whitehead, G. W.On the (n + 2)nd homotopy group of the n-sphere. Ann. Math., Princeton (2), 52 (1950), 245–7.CrossRefGoogle Scholar