Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
CUTKOSKY, STEVEN DALE
HERZOG, JÜRGEN
and
SRINIVASAN, HEMA
2010.
Asymptotic growth of algebras associated to powers of ideals.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 148,
Issue. 1,
p.
55.
Trung, N.V.
and
Verma, J.K.
2010.
Hilbert functions of multigraded algebras, mixed multi- plicities of ideals and their applications.
Journal of Commutative Algebra,
Vol. 2,
Issue. 4,
ULRICH, BERND
and
VALIDASHTI, JAVID
2011.
Numerical criteria for integral dependence.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 151,
Issue. 1,
p.
95.
Hoa, Lê Tuân
and
Morales, Marcel
2012.
Non-linear behaviour of Castelnuovo–Mumford regularity.
Journal of Algebra,
Vol. 356,
Issue. 1,
p.
207.
Cutkosky, Steven
2013.
Multiplicities associated to graded families of ideals.
Algebra & Number Theory,
Vol. 7,
Issue. 9,
p.
2059.
Katz, Daniel
and
Puthenpurakal, Tony J.
2013.
Quasi-finite modules and asymptotic prime divisors.
Journal of Algebra,
Vol. 380,
Issue. ,
p.
18.
Cutkosky, Steven Dale
2014.
Asymptotic multiplicities of graded families of ideals and linear series.
Advances in Mathematics,
Vol. 264,
Issue. ,
p.
55.
Ciupercă, Cătălin
2015.
Asymptotic growth of multiplicity functions.
Journal of Pure and Applied Algebra,
Vol. 219,
Issue. 4,
p.
1045.
Cutkosky, Steven Dale
2015.
Asymptotic multiplicities.
Journal of Algebra,
Vol. 442,
Issue. ,
p.
260.
Hà, Huy Tài
and
Vinh, Pham An
2016.
Growth of multiplicities of graded families of ideals.
Journal of Algebra,
Vol. 452,
Issue. ,
p.
311.
Ciupercă, Cătălin
2016.
Degrees of multiplicity functions for equimultiple ideals.
Journal of Algebra,
Vol. 452,
Issue. ,
p.
106.
Arkian, Seyed Shahab
2017.
Higher Iterated Hilbert Coefficients of the Graded Components of Bigraded Modules.
Algebra Colloquium,
Vol. 24,
Issue. 04,
p.
551.
Dao, Hailong
and
Montaño, Jonathan
2018.
Length of local cohomology of powers of ideals.
Transactions of the American Mathematical Society,
Vol. 371,
Issue. 5,
p.
3483.
Cường, Đoàn Trung
Nam, Phạm Hồng
and
Quý, Phạm Hùng
2018.
On the Length Function of Saturations of Ideal Powers.
Acta Mathematica Vietnamica,
Vol. 43,
Issue. 2,
p.
275.
Nguyen, Hop D.
and
Vu, Thanh
2019.
Homological Invariants of Powers of Fiber Products.
Acta Mathematica Vietnamica,
Vol. 44,
Issue. 3,
p.
617.
CALLEJAS-BEDREGAL, R.
PÉREZ, V. H. JORGE
and
FERRARI, M. DUARTE
2019.
On coefficient ideals.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 167,
Issue. 02,
p.
285.
Sarkar, Parangama
2020.
Rees' theorem for filtrations, multiplicity function and reduction criteria.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 2,
p.
789.
Jorge Pérez, V.H.
and
Lima, P.H.
2020.
Asymptotic behavior of coefficient ideals.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 4,
p.
106219.
Dao, Hailong
and
Montaño, Jonathan
2020.
On asymptotic vanishing behavior of local cohomology.
Mathematische Zeitschrift,
Vol. 295,
Issue. 1-2,
p.
73.
Busé, Laurent
Cid‐Ruiz, Yairon
and
D'Andrea, Carlos
2020.
Degree and birationality of multi‐graded rational maps.
Proceedings of the London Mathematical Society,
Vol. 121,
Issue. 4,
p.
743.
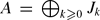 and
and  are finitely generated, we show the function k ↦ e0(Ik/Jk) is of quasi-polynomial type, say given by the polynomials P0,. . ., Pg−1. If Jk = Jk for all k, for a graded ideal J, then we show that all the Pi have the same degree and the same leading coefficient. As one of the applications it is shown that
are finitely generated, we show the function k ↦ e0(Ik/Jk) is of quasi-polynomial type, say given by the polynomials P0,. . ., Pg−1. If Jk = Jk for all k, for a graded ideal J, then we show that all the Pi have the same degree and the same leading coefficient. As one of the applications it is shown that 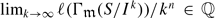 , if I is a monomial ideal. We also study analogous statements in the local case.
, if I is a monomial ideal. We also study analogous statements in the local case.