Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-30T21:33:17.428Z Has data issue: false hasContentIssue false
  • English
  • Français

Hereditary quasirandomness without regularity

Published online by Cambridge University Press:  26 January 2017

DAVID CONLON ,
JACOB FOX  and
BENNY SUDAKOV
DAVID CONLON
Affiliation:
Mathematical Institute, Oxford OX2 6GG, United Kingdom. e-mail: [email protected]
JACOB FOX
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, U.S.A. e-mail: [email protected]
BENNY SUDAKOV
Affiliation:
Department of Mathematics, ETH, 8092 Zurich, Switzerland. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A result of Simonovits and Sós states that for any fixed graph H and any ε > 0 there exists δ > 0 such that if G is an n-vertex graph with the property that every S ⊆ V(G) contains pe(H) |S|v(H) ± δ nv(H) labelled copies of H, then G is quasirandom in the sense that every S ⊆ V(G) contains 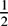$\frac{1}{2}$p|S|2± ε n2 edges. The original proof of this result makes heavy use of the regularity lemma, resulting in a bound on δ−1 which is a tower of twos of height polynomial in ε−1. We give an alternative proof of this theorem which avoids the regularity lemma and shows that δ may be taken to be linear in ε when H is a clique and polynomial in ε for general H. This answers a problem raised by Simonovits and Sós.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 164 , Issue 3 , May 2018 , pp. 385 - 399
Copyright
Copyright © Cambridge Philosophical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Chung, F. R. K., Graham, R. L. and Wilson, R. M. Quasi-random graphs. Combinatorica 9 (1989), 345–362.Google Scholar
[2] Conlon, D. A new upper bound for diagonal Ramsey numbers. Ann. of Math. 170 (2009), 941–960.CrossRefGoogle Scholar
[3] Conlon, D. and Fox, J. Bounds for graph regularity and removal lemmas. Geom. Funct. Anal. 22 (2012), 1191–1256.Google Scholar
[4] Conlon, D., Fox, J. and Sudakov, B. An approximate version of Sidorenko's conjecture. Geom. Funct. Anal. 20 (2010), 1354–1366.Google Scholar
[5] Conlon, D., Kim, J. H., Lee, C. and Lee, J. Some advances on Sidorenko's conjecture. arXiv:1510.06533 [math.CO].Google Scholar
[6] Erdős, P., Goldberg, M., Pach, J. and Spencer, J. Cutting a graph into two dissimilar halves. J. Graph Theory 12 (1988), 121–131.Google Scholar
[7] Gowers, W. T. A new proof of Szemerédi's theorem. Geom. Funct. Anal. 11 (2001), 465–588.CrossRefGoogle Scholar
[8] Hoory, S., Linial, N. and Wigderson, A. Expander graphs and their applications. Bull. Amer. Math. Soc. 43 (2006), 439–561.Google Scholar
[9] Janson, S., Łuczak, T. and Ruciński, A. Random graphs. (Wiley, New York, 2000).Google Scholar
[10] Katona, G. A theorem of finite sets. Theory of graphs (Proc. Colloq., Tihany, 1966) (Academic Press, New York, 1968), 187–207.Google Scholar
[11] Kim, J. H., Lee, C. and Lee, J. Two approaches to Sidorenko's conjecture. Trans. Amer. Math. Soc. 368 (2016), 5057–5074.CrossRefGoogle Scholar
[12] Krivelevich, M. and Sudakov, B. Pseudo-random graphs. More sets, graphs and numbers. Bolyai Soc. Math. Stud. 15 (Springer, Berlin, 2006), 199–262.Google Scholar
[13] Kruskal, J. B. The number of simplices in a complex. Mathematical optimization techniques, (Univ. of California Press, Berkeley, Calif., 1963), 251–278.Google Scholar
[14] Li, J. X. and Szegedy, B. On the logarithmic calculus and Sidorenko's conjecture. To appear in Combinatorica.Google Scholar
[15] Lovász, L. Combinatorial Problems and Exercises, 2nd edition (AMS Chelsea Publishing, Providence, RI, 2007).Google Scholar
[16] Lovász, L. Large networks and graph limits. Amer. Math. Soc. Colloq. Publ., vol. 60 (Amer. Math. Soc., Providence, RI, 2012).CrossRefGoogle Scholar
[17] Lovász, L. and Szegedy, B. Szemerédi's lemma for the analyst. Geom. Funct. Anal. 17 (2007), 252–270.Google Scholar
[18] Reiher, C. and Schacht, M. in preparation.Google Scholar
[19] Shapira, A. Quasi-randomness and the distribution of copies of a fixed graph. Combinatorica 28 (2008), 735–745.Google Scholar
[20] Simonovits, M. and Sós, V. T. Hereditarily extended properties, quasi-random graphs and not necessarily induced subgraphs. Combinatorica 17 (1997), 577–596.Google Scholar
[21] Skokan, J. and Thoma, L. Bipartite subgraphs and quasi-randomness. Graphs Combin. 20 (2004), 255–262.Google Scholar
[22] Szegedy, B. An information theoretic approach to Sidorenko's conjecture. arXiv:1406.6738v3 [math.CO].Google Scholar
[23] Szemerédi, E. Regular partitions of graphs. Problèmes combinatoires et théorie des graphes (Colloq. Internat. CNRS, Univ. Orsay, Orsay, 1976), 399–401. Colloq. Internat. CNRS, vol. 260 (CNRS, Paris, 1978).Google Scholar
[24] Thomason, A. Pseudorandom graphs. Random graphs '85 (Poznań, 1985) North-Holland Math. Stud. 144 (North-Holland, Amsterdam, 1987), 307–331.Google Scholar
[25] Thomason, A. Random graphs, strongly regular graphs and pseudorandom graphs. Surveys in Combinatorics 1987 (New Cross, 1987), 173–195. London Math. Soc. Lecture Note Ser. 123 (Cambridge University Press, Cambridge, 1987).Google Scholar