No CrossRef data available.
Harmonic conjugation in L1 on compact abelian groups
Published online by Cambridge University Press: 24 October 2008
Extract
Let G denote a compact connected abelian group with character groupand normalized Haar measure . As a consequence of the duality theorems (11, theorem 2518),is torsion-free and hence can be ordered. That is, there is a sub-semigroup P ofsuch that
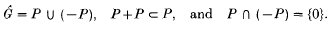
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 111 , Issue 1 , January 1992 , pp. 113 - 126
- Copyright
- Copyright © Cambridge Philosophical Society 1992
References
REFERENCES
1Asmar, N.. The conjugate function on the finite dimensional torus. Canad. Math. Bull. 32 (1989), 140148.Google Scholar
2Asmar, N., Berkson, E. and Gillespie, T. A.. Representation of groups with ordered duals and generalized analyticity. J. Fund. Anal. 90 (1990), 206235.Google Scholar
3Asmar, N., Berkson, E. and Gillespie, T. A.. Distributional control and generalized analyticity. Integral Equations Operator Theory, 14 (1991), 311341.Google Scholar
4Asmar, N. and Hewitt, E.. Marcel Riesz's theorem on conjugate Fourier series and its descendants. In Proceedings of the Analysis Conference (Singapore 1986) (editors Choy, S. T. L. et al. ) (Elsevier Science Publishers, 1988), pp. 156Google Scholar
5Berkson, E. and Gillespie, T. A.. The generalized M. Riesz Theorem and transference. Pacific J. Math. 120 (1985), 279288.Google Scholar
6Caldern, A. P.. Ergodic theory and translation-invariant operators. Proc. Nat. Acad. Sci. U.S.A. 59 (1968), 349353.Google Scholar
7Coifman, R. R. and Weiss, G.. Maximal functions and Hp spaces defined by ergodic transformations. Proc. Nat. Acad. Sci. U.S.A. 70 (1973), 17611763.Google Scholar
8Coifman, R. R. and Weiss, G.. Transference Methods in Analysis. Regional Conference Ser Math. no. 31 (American Mathematical Society, 1977).Google Scholar
10Hewitt, E. and Koshi, S.. Orderings in locally compact Abelian groups and the theorem of F. and M. Riesz. Math. Proc. Cambridge Philos. Soc. 93 (1983), 441457.Google Scholar
11Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis, vol. 1 (Springer-Verlag, 1963).Google Scholar
12Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis, vol. 2 (Springer-Verlag, 1970).Google Scholar
15Zygmund, A.. Trigonometric Series, 2nd edition, 2 vols. (Cambridge University Press, 1959).Google Scholar


