1. Any mention of the word ‘grouping’ immediately brings to a statistician's mind the Sheppard corrections. These are usually used to make inferences about the underlying ungrouped population from observations made on the grouped population, but it is important to realize that, as stated and proved, they have nothing to do with sampling or inference and are merely expressions for the moments of one population in terms of the moments of another population derived from it. They can only be used for the inference problem when allied to the method of moments. This method, as formulated by K. Pearson, consists in taking for θ* the estimate of the population parameter θ, the same function of the sample moments mi that θ is of the population moments μi, each mi being an estimate of the corresponding μi. If the population is grouped the mi are estimates of the 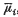, the grouped population moments, so we require θ as a function of the 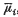to apply Pearson's method. This can be done since θ is known as a function of the µi and the µi are known as functions of the 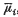by the corrections. Use of the Sheppard corrections with any other inference method, even when this method, when applied to the continuous population, yields an estimate which is a sample moment, so far as I am aware, has not been examined except for the normal curve.