Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T02:51:20.291Z Has data issue: false hasContentIssue false
  • English
  • Français

A Geometrical treatment of the Correspondence between Lines in Threefold Space and Points of a Quadric in Fivefold space

Published online by Cambridge University Press:  24 October 2008

H. W. Turnbull
H. W. Turnbull
Affiliation:
Trinity College.
Get access Rights & Permissions [Opens in a new window]

Extract

§ 1. The six Plücker coordinates of a straight line in three dimensional space satisfy an identical quadratic relation

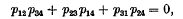
which immediately shows that a one-one correspondence may be set up between lines in three dimensional space, λ, and points on a quadric manifold 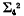of four dimensions in five dimensional space, S5. For these six numbers pij may be considered to be six homogeneous coordinates of such a point.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 5 , July 1925 , pp. 694 - 699
Copyright
Copyright © Cambridge Philosophical Society 1925

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* It seems unnecessary here to develop the pure geometrical theory of negative circles in full. It corresponds to the analytical fact that a locus

exists where g, f, c are real and g2 + f2 < c.

† Cf. Baker, , Principles of Geometry, I (Cambridge, 1922), 165–172, 182.Google Scholar

* One system of generators of an ordinary ruled quadrio surface.