In the early editions of the Geometry of Three Dimensions Salmon had stated that the equations of any three quadric surfaces could be simultaneously reduced to the sums of five squares. Such a reduction is not possible in general, but can be performed if and only if a certain combinant Λ, of the net of quadrics, vanishes. Algebraically the theory of such a net of quadrics is equivalent, as Hesse(2) showed, to that of a plane quartic curve: and the condition for the equation a quartic to be expressible to the sum of five fourth powers is equivalent to the condition Λ = 0(1). While Clebsch(3) was the first to establish this condition, Lüroth(4) gave it more explicit form by studying the quartic curve

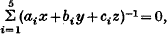
which satisfies the condition. Frahm(5) seems to have been the first to prove the impossibility of the above reduction of three general quadric surfaces, by remarking that the plane quartic curve obtained in Hesse's way from the locus of the vertices of cones of the net of quadrics would be a Lüroth quartic. Frahm further remarked that the three quadrics, so conditioned, could be regarded as the polar quadrics belonging to a cubic surface in ∞2 ways; but that for three general quadrics no such cubic surface exists. An explicit algebraical account of these properties was given by E. Toeplitz(6), who incidentally noticed that certain linear complexes associated with three general quadrics became special linear complexes when Λ = 0. This polar property of three quadrics in [3] was generalized to n dimensions by Anderson (7).