Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T14:17:22.230Z Has data issue: false hasContentIssue false
  • English
  • Français

Generic bifurcations of forced oscillations of integrable mechanical systems

Published online by Cambridge University Press:  24 October 2008

J. P. Cleave
J. P. Cleave
Affiliation:
University of Bristol
Get access Rights & Permissions [Opens in a new window]

Extract

Although integrable Hamiltonian systems are non-generic (Robinson (13)) they have some importance in classical mechanics, e.g. the two-body problem, a free rigid body not subject to a gravitational field, the Toda lattice (Moser(12)). Arnol'd (cf. (2) and (1), appendix 26) proved that under quite general conditions action-angle coordinates can be introduced. Accordingly we consider a fixed system 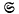with n degrees of freedom in the standard form

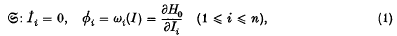
where H0 is a smooth function of the action variables Li only and I ∈ I and I is an open set of n-tuples of positive reals. 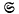now subjected to a periodic impressed force, the resulting system, 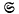, being determined by a small, periodic perturbation of the energy function

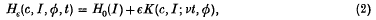
where e is a small positive real and K(c, I; α0, α1, …, an) is a smooth function of parameters c ranging over a smooth r-manifold E, I ∈ I, and K has period 2π in each of the angles αi, i.e. (α0, …, αn) ∈ Tn (n-torus). The purpose of this paper is to define the forms of bifurcation of oscillations of the perturbed system 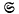(K):

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 85 , Issue 1 , January 1979 , pp. 125 - 142
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Arnol'd, V. I. and Avez, A.Ergodic problems of classical mechanics (New York, Benjamin, 1968).Google Scholar
(2)Arnol'd, V. I.Ob odnoi teoreme Liuvilya kasayusheiya integriruyemykh problem dinamiki. Sib. Mat. J. 4 (1963).Google Scholar
(3)Arnol'd, V. I.Normal forms for functions near degenerate critical points, the Weyl groups of Ak, Dk, Ek and Lagrangian singularities. Funktsional Anal. i Priložhen. 6 (1972), 3–25.Google Scholar
(4)Arnol'd, V. I.Proof of a theorem of A. N. Kolmogorov on the invariance of quasi-periodicmotions under small perturbation of the Hamiltonian. Uspehi Mat. Nauk 18 (1963), 13–40. (Also Russian Math Surveys 18 (1963), 9–36.)Google Scholar
(5)Berger, M. S. and Berger, M. S., Perspectives in non-linearity (Benjamin, 1968).Google Scholar
(6)Brocker, Th.Differentiable germs and catastrophes (London Math. Soc. Lecture Notes Series, no. 17, Cambridge University Press, 1975).Google Scholar
(7)Chester, W.The forced oscillations of a simple pendulum. J. Inst. Math. Appl. 15 (1975), 289–306.CrossRefGoogle Scholar
(8)Eells, J.Singularities of smooth maps (London, Nelson, 1968).Google Scholar
(9)Golubitsky, M. and Guillemin, V.Stable mappings and their singularities (New York, Springer–Verlag, 1973).CrossRefGoogle Scholar
(10)Hale, J.Ordinary differential equations (New York, Wiley, 1969).Google Scholar
(11)Meyer, K. R.Generic bifurcation of periodic points. Trans. Amer. Math. Soc. 149 (1970), 95–107.CrossRefGoogle Scholar
(12)Moser, J. Finitely many mass points on the line under the influence of an exponential potential – an integrable system. In Dynamical systems, theory and applications (Lecture Notes in Physics, no. 38, Springer, 1975).Google Scholar
(13)Robinson, R. C.Generic properties of conservative systems. Amer. J. Math. 92 (1970), 562–603.Google Scholar
(14)Trotman, D. and Zeeman, E. C. The classification of elementary catastrophes of codimension 5. In Catastrophe Theory – Seattle 1975 (Lecture Notes in Math. no. 525, Berlin–Heidelberg, Springer–Verlag, 1976).Google Scholar