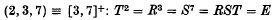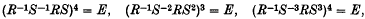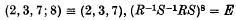Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Leech, John
1966.
Note on the abstract group (2,3,7;9).
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 62,
Issue. 1,
p.
7.
Cannon, John J.
1969.
Computers in group theory.
Communications of the ACM,
Vol. 12,
Issue. 1,
p.
3.
NEUBÜSER, J.
1970.
Computational Problems in Abstract Algebra.
p.
1.
LEECH, JOHN
1970.
Computational Problems in Abstract Algebra.
p.
21.
Chunikhin, S. A.
and
Shemetkov, L. A.
1973.
Finite groups.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 3,
p.
291.
Cannon, John J.
Dimino, Lucien A.
Havas, George
and
Watson, Jane M.
1973.
Implementation and analysis of the Todd-Coxeter algorithm.
Mathematics of Computation,
Vol. 27,
Issue. 123,
p.
463.
Cohen, Jeffrey M.
1979.
On Hurwitz extensions by PSL2(7).
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 86,
Issue. 3,
p.
395.
Cohen, Jeffrey
1981.
The Geometric Vein.
p.
511.
Cohen, Jeffrey
1981.
On non-Hurwitz groups and non-congruence subgroups of the modular group.
Glasgow Mathematical Journal,
Vol. 22,
Issue. 1,
p.
1.
Cohen, Jeffrey
1984.
Homomorphisms of cocompact Fuchsian groups on 𝑃𝑆𝐿₂(𝑍_{𝑝ⁿ}[𝑥]/(𝑓(𝑥))).
Transactions of the American Mathematical Society,
Vol. 281,
Issue. 2,
p.
571.
Conder, Marston
1986.
A family of Hurwitz groups with non-trivial centres.
Bulletin of the Australian Mathematical Society,
Vol. 33,
Issue. 1,
p.
123.
Bergau, Peter
and
Garbe, D.
1989.
Groups — Korea 1988.
Vol. 1398,
Issue. ,
p.
29.
Conder, Marston
1990.
Hurwitz groups: A brief survey.
Bulletin of the American Mathematical Society,
Vol. 23,
Issue. 2,
p.
359.
Turbek, Peter S.
1993.
On compact Riemann surfaces with a maximal number of automorphisms.
Manuscripta Mathematica,
Vol. 80,
Issue. 1,
p.
113.
Campbell, C. M.
Conder, M. D. E.
and
Robertson, E. F.
1994.
Defining-relations for Hurwitz groups.
Glasgow Mathematical Journal,
Vol. 36,
Issue. 3,
p.
363.
Tamburini, M.C.
and
Vsemirnov, M.
2006.
Vol. 4,
Issue. ,
p.
385.
Conder, Marston D.E.
and
Ma, Jicheng
2013.
Arc-transitive abelian regular covers of cubic graphs.
Journal of Algebra,
Vol. 387,
Issue. ,
p.
215.
Vsemirnov, Maxim
2018.
On the primitive divisors of the recurrent sequence
$$u_{n+1}=(4\rm{cos}^2(2\pi/7)-1)\it{u}_{n}-u_{n-\rm{1}}$$
u
n
+
1
=
(
4
c
o
s
2
(
2
π
/
7
)
−
1
)
u
n
−
u
n
−
1
with applications to group theory.
Science China Mathematics,
Vol. 61,
Issue. 11,
p.
2101.
Schein, Michael M.
and
Shoan, Amir
2022.
Systolic length of triangular modular curves.
Journal of Number Theory,
Vol. 239,
Issue. ,
p.
462.