Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-30T21:28:10.370Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized triangle groups

Published online by Cambridge University Press:  24 October 2008

Gilbert Baumslag ,
John W. Morgan  and
Peter B. Shalen
Gilbert Baumslag
Affiliation:
Department of Mathematics, City College, New York, NY 10031, U.S.A.
John W. Morgan
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027, U.S.A.
Peter B. Shalen
Affiliation:
Department of Mathematics, University of Illinois at Chicago, Chicago, IL 60680, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

A group G is called a triangle group if it can be presented in the form

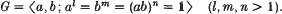
It is well-known that G is isomorphic to a subgroup of PSL2(ℂ), that a is of order l, b is of order m and ab is of order n. If

then G contains the fundamental group of a positive genus orientable surface as a subgroup of finite index whenever s(G) ≤ 1; in particular G is infinite. Furthermore, if s(G) < 1, the genus of the surface is greater than 1 and consequently G contains a free group of rank 2.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 1 , July 1987 , pp. 25 - 31
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baumslag, B. and Pride, S. J.. Groups with two more generators than relators. J. London Math. Soc. (2) 17 (1978), 425–426.CrossRefGoogle Scholar
[2] Boyer, S.. On proper powers in free products and Dehn surgery. Preprint (1986).Google Scholar
[3] Culler, M. and Shalen, P. B.. Varieties of group representations and splittings of 3-manifolds. Annals of Math. 117 (1983), 109–146.CrossRefGoogle Scholar
[4] González-Acuña, F. and Short, H.. Knot surgery and primeness. Math. Proc. Cambridge Philos. Soc. 99 (1986), 89–102.CrossRefGoogle Scholar
[5] McA. Gordon, C. and Luecke, J.. Only integral Dehn surgeries can yield reducible manifolds. Math. Proc. Cambridge Philos. Soc. 102 (1987), 97–101.CrossRefGoogle Scholar
[6] Horowitz, R.. Characters of free groups represented in the two-dimensional linear group. Comm. Pure & Appl. Math. 25 (1972), 635–649.CrossRefGoogle Scholar
[7] Kurosh, A. G.. Die Untergruppen der freien Produkte von beliebigen Gruppen. Math. Ann. 109 (1934), 647–660.CrossRefGoogle Scholar
[8] Lubotzky, A. and Magid, A.. Varieties of representations of finitely generated groups. To appear.Google Scholar
[9] Mal'cev, A. I.. On faithful representations of infinite groups of matrices. American Math. Soc. Translations (2) 45 (1965), 1–18.CrossRefGoogle Scholar
[10] Ree, R. and Mendelsohn, N. S.. Free subgroups of groups with a single defining relation. Arch. Math. 19 (1968), 577–580.CrossRefGoogle Scholar
[11] Wall, C. T. C.. Rational Euler characteristics. Proc. Cambridge Philos. Soc. 57 (1961), 182–184.CrossRefGoogle Scholar