Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zakeri, H.
1986.
d
‐sequences, local cohomology modules and generalized analytic independence
.
Mathematika,
Vol. 33,
Issue. 2,
p.
279.
Sharp, R. Y.
and
Yassi, M.
1990.
Generalized fractions and Hughes' gradetheoretic analogue of the Cousin complex.
Glasgow Mathematical Journal,
Vol. 32,
Issue. 2,
p.
173.
Chung, Sang-Cho
1994.
Complexes of Cousin type and modules of generalized fractions.
Nagoya Mathematical Journal,
Vol. 136,
Issue. ,
p.
17.
Khashyarmanesh, K.
Salarian, Sh.
and
Zakeri, H.
1998.
Characterizations of filter regular sequences and unconditioned strong d-sequences.
Nagoya Mathematical Journal,
Vol. 151,
Issue. ,
p.
37.
Dibaei, Mohammad T.
2005.
A STUDY OF COUSIN COMPLEXES THROUGH THE DUALIZING COMPLEXES.
Communications in Algebra,
Vol. 33,
Issue. 1,
p.
119.
Huneke, Craig
Katzman, Mordechai
Sharp, Rodney Y.
and
Yao, Yongwei
2006.
Frobenius test exponents for parameter ideals in generalized Cohen–Macaulay local rings.
Journal of Algebra,
Vol. 305,
Issue. 1,
p.
516.
Katzman, Mordechai
and
Sharp, Rodney
2022.
Lyubeznik numbers, 𝐹-modules and modules of generalized fractions.
Transactions of the American Mathematical Society,


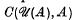 of
of 