Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T23:37:51.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Bianchi identities for horizontal distributions

Published online by Cambridge University Press:  24 October 2008

M. Crampin
M. Crampin
Affiliation:
The Open University, Walton Hall, Milton Keynes
Get access Rights & Permissions [Opens in a new window]

Extract

A linear connection on a differentiable manifold M defines a horizontal distribution on the tangent bundle T(M). Horizontal distributions on tangent bundles are of some interest even when they are not generated by connections. Much of linear connection theory generalizes to arbitrary horizontal distributions. In particular, there are generalized versions of Bianchi's two identities for the torsion T and curvature R

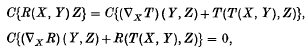
where C denotes the cyclic sum with respect to X, Y and Z. These identities are derived below by associating with a horizontal distribution a graded derivation of degree 1 in a graded Lie algebra of vertical forms on M. This approach reveals the fundamentally algebraic origin of the Bianchi identities.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 94 , Issue 1 , July 1983 , pp. 125 - 132
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Corwin, L., Ne'eman, Y. and Sternberg, S.Graded Lie algebras in mathematics and physics (Bose-Fermi symmetry). Rev. Modern Phys. 47 (1975), 573–603.CrossRefGoogle Scholar
(2)Crampin, M.On horizontal distributions on the tangent bundle of a differential manifold. J. London Moth. Soc. (2), 3 (1971), 178–182.CrossRefGoogle Scholar
(3)Crampin, M.On the differential geometry of the Euler-Lagrange equations, and the inverse problem of Lagrangian dynamics. J. Phys. A 14 (1981), 2567–2575.Google Scholar
(4)Crampin, M.Tangent bundle geometry for Lagrangian dynamics. (Preprint, Open University, 1983.)CrossRefGoogle Scholar
(5)Hermann, R.Gauge fields and Cartan-Ehresmann connections, Part A (Interdisciplinary Mathematics, vol. X: Math. Sci. Press, Brookline, Mass., 1975).Google Scholar
(6)Yano, K. and Ishihara, S.Tangent and cotangent bundles. (Marcel Dekker Inc., New York 1973).Google Scholar