Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Luther, Wolfram
1977.
The remainder in a gap Tauberian theorem for Abel summability.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 81,
Issue. 1,
p.
43.
Mel'nik, V. I.
1979.
Tauberian theorems for Summation methods of abel type.
Ukrainian Mathematical Journal,
Vol. 31,
Issue. 2,
p.
109.
Jakimovski, A.
Meyer-König, W.
and
Zeller, K.
1981.
Power series methods of summability: positivity and gap perfectness.
Transactions of the American Mathematical Society,
Vol. 266,
Issue. 1,
p.
309.
Sarvothaman, K.
1983.
A gap Tauberian theorem for generalised absolute Abel summability.
Proceedings of the American Mathematical Society,
Vol. 89,
Issue. 4,
p.
651.
Tietz, Hubert
and
Trautner, Rolf
1988.
Tauber-S�tze f�r Potenzreihenverfahren.
Archiv der Mathematik,
Vol. 50,
Issue. 2,
p.
164.
Tietz, Hubert
and
Zeller, Karl
1999.
Charakterisierung von O-Tauber-Bedingungen für Teilwirkfelder mit Abschnittskonvergenz.
Results in Mathematics,
Vol. 35,
Issue. 3-4,
p.
380.


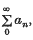 write
write