Published online by Cambridge University Press: 28 September 2009
Let f(x) ∈ 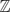 [x] be a monic irreducible reciprocal polynomial of degree 2d with roots r1, 1/r1, r2, 1/r2, . . ., rd, 1/rd. The corresponding trace polynomial g(x) of degree d is the polynomial whose roots are r1 + 1/r1, . . ., rd + 1/rd. If the Galois groups of f and g are Gf and Gg respectively, then Gg ≅ Gf/N, where N is isomorphic to a subgroup of C2d. In a naive sense, the generic case is Gf ≅ C2d ⋊ Sd, with N ≅ C2d and Gg ≅ Sd. When f(x) has extra structure this may be reflected in the Galois group, and it is not always true even that Gf ≅ N ⋊ Gg. For example, for cyclotomic polynomials f(x) = Φn(x) it is known that Gf ≅ N ⋊ Gg if and only if n is divisible either by 4 or by some prime congruent to 3 modulo 4.
[x] be a monic irreducible reciprocal polynomial of degree 2d with roots r1, 1/r1, r2, 1/r2, . . ., rd, 1/rd. The corresponding trace polynomial g(x) of degree d is the polynomial whose roots are r1 + 1/r1, . . ., rd + 1/rd. If the Galois groups of f and g are Gf and Gg respectively, then Gg ≅ Gf/N, where N is isomorphic to a subgroup of C2d. In a naive sense, the generic case is Gf ≅ C2d ⋊ Sd, with N ≅ C2d and Gg ≅ Sd. When f(x) has extra structure this may be reflected in the Galois group, and it is not always true even that Gf ≅ N ⋊ Gg. For example, for cyclotomic polynomials f(x) = Φn(x) it is known that Gf ≅ N ⋊ Gg if and only if n is divisible either by 4 or by some prime congruent to 3 modulo 4.
In this paper we deal with irreducible reciprocal monic polynomials f(x) ∈ 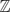 [x] that are ‘close’ to being cyclotomic, in that there is one pair of real positive reciprocal roots and all other roots lie on the unit circle. With the further restriction that f(x) has degree at least 4, this means that f(x) is the minimal polynomial of a Salem number. We show that in this case one always has Gf ≅ N ⋊ Gg, and moreover that N ≅ C2d or C2d−1, with the latter only possible if d is odd.
[x] that are ‘close’ to being cyclotomic, in that there is one pair of real positive reciprocal roots and all other roots lie on the unit circle. With the further restriction that f(x) has degree at least 4, this means that f(x) is the minimal polynomial of a Salem number. We show that in this case one always has Gf ≅ N ⋊ Gg, and moreover that N ≅ C2d or C2d−1, with the latter only possible if d is odd.