In our previous consideration in (1) of the constant-coefficient fifth-order differential equation:

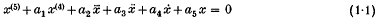
an attempt was made to identify (though not exhaustively) different sufficient conditions on a1,…,a5 for the instability of the trivial solution x = 0 of (1·1). It was our expectation that the conditions so identified could be generalized in some form or other to equations (1·1) in which a1,…,a5 were not necessarily constants, thereby giving rise to instability theorems for some non-linear fifth-order differential equations; and this turned out in fact to be so except only for the case:

with R0 = R0(a1, a2, a3, a4) > 0 sufficiently large, about which we were unable at the time to derive any worthwhile generalization to any equation (1·1) in which a1, …,a5 are not all constants.