No CrossRef data available.
Article contents
Free quotients of subgroups of the Bianchi groups whose kernels contain many elementary matrices
Published online by Cambridge University Press: 24 October 2008
Abstract
Let d be a square-free positive integer and let 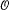 be the ring of integers of the imaginary quadratic number field ℚ(√ − d) The Bianchi groups are the groups SL2(
be the ring of integers of the imaginary quadratic number field ℚ(√ − d) The Bianchi groups are the groups SL2(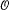 ) (or PSL2(
) (or PSL2(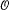 ). Let
). Let 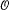 m be the order of index m in
m be the order of index m in 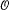 . In this paper we prove that for each d there exist infinitely many m for which SL2(
. In this paper we prove that for each d there exist infinitely many m for which SL2(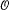 m)/NE2(
m)/NE2(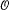 m) has a free, non-cyclic quotient, where NE2(
m) has a free, non-cyclic quotient, where NE2(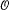 m) is the normal subgroup of SL2(
m) is the normal subgroup of SL2(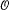 m) generated by the elementary matrices. When d is not a prime congruent to 3 (mod 4) this result is true for all but finitely many m. The proofs are based on the fundamental paper of Zimmert and its generalization due to Grunewald and Schwermer.
m) generated by the elementary matrices. When d is not a prime congruent to 3 (mod 4) this result is true for all but finitely many m. The proofs are based on the fundamental paper of Zimmert and its generalization due to Grunewald and Schwermer.
The results are used to extend earlier work of Lubotzky on non-congruence subgroups of SL2(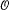 ), which involves the concept of the ‘non-congruence crack’. In addition the results highlight a number of low-dimensional anomalies. For example, it is known that [SLn(
), which involves the concept of the ‘non-congruence crack’. In addition the results highlight a number of low-dimensional anomalies. For example, it is known that [SLn(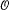 m), SLn
m), SLn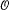 m)] = En(
m)] = En(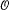 m), when n ≥ 3, where [SLn(
m), when n ≥ 3, where [SLn(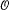 m), SLn(
m), SLn(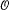 m)] is the commutator subgroup of SL(
m)] is the commutator subgroup of SL(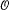 m) and En(
m) and En(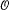 m) is the subgroup of SLn(
m) is the subgroup of SLn(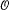 m) generated by the elementary matrices. Our results show that this is not always true when n = 2.
m) generated by the elementary matrices. Our results show that this is not always true when n = 2.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 116 , Issue 2 , September 1994 , pp. 253 - 273
- Copyright
- Copyright © Cambridge Philosophical Society 1994


