Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T20:42:36.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Free actions of p-groups on affine varieties in characteristic p

Published online by Cambridge University Press:  04 April 2017

PETER FLEISCHMANN  and
CHRIS WOODCOCK
PETER FLEISCHMANN
Affiliation:
School of Mathematics, Statistics and Actuarial Science, University of Kent, Canterbury, CT2 7FS e-mails: [email protected]; [email protected]
CHRIS WOODCOCK
Affiliation:
School of Mathematics, Statistics and Actuarial Science, University of Kent, Canterbury, CT2 7FS e-mails: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be an algebraically closed field and 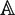$\mathbb{A}$n ≅ Kn affine n-space. It is known that a finite group 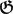$\frak{G}$ can only act freely on 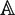$\mathbb{A}$n if K has characteristic p > 0 and 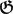$\frak{G}$ is a p-group. In that case the group action is “non-linear” and the ring of regular functions K[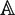$\mathbb{A}$n] must be a trace-surjectiveK − 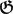$\frak{G}$-algebra.

Now let k be an arbitrary field of characteristic p > 0 and let G be a finite p-group. In this paper we study the category 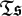$\mathfrak{Ts}$ of all finitely generated trace-surjective k − G algebras. It has been shown in [13] that the objects in 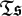$\mathfrak{Ts}$ are precisely those finitely generated k − G algebras A such that AG ≤ A is a Galois-extension in the sense of [7], with faithful action of G on A. Although 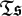$\mathfrak{Ts}$ is not an abelian category it has “s-projective objects”, which are analogues of projective modules, and it has (s-projective) categorical generators, which we will describe explicitly. We will show that s-projective objects and their rings of invariants are retracts of polynomial rings and therefore regular UFDs. The category 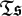$\mathfrak{Ts}$ also has “weakly initial objects”, which are closely related to the essential dimension of G over k. Our results yield a geometric structure theorem for free actions of finite p-groups on affine k-varieties. There are also close connections to open questions on retracts of polynomial rings, to embedding problems in standard modular Galois-theory of p-groups and, potentially, to a new constructive approach to homogeneous invariant theory.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 165 , Issue 1 , July 2018 , pp. 109 - 135
Copyright
Copyright © Cambridge Philosophical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Auslander, M. and Goldmann, O. The Brauer group of a commutative ring. Trans. Amer. Math. Soc. 97 (1960), 367–409.Google Scholar
[2] Berhuy, G. and Favi, G. Essential Dimension: A functorial point of view (after A Merkurjev). Documenta Mathematica 8 (2003), 270–330.Google Scholar
[3] Bourbaki, N.. Groupes et Algèbres de Lie, chapters IV,V,VI (Herman, Paris, 1968).Google Scholar
[4] Bruns, W. and Herzog, J. Cohen–Macaulay Rings (Cambridge University Press, 1993).Google Scholar
[5] Buhler, J. and Reichstein, Z. On the essential dimension of a finite group. Compos Math. 106 (1997), 159–179.Google Scholar
[6] Kang, M. C. Essential dimensions of finite groups. arXiv.math: 0611673v2 (2006), 1–24.Google Scholar
[7] Chase, S. U., Harrison, D. K. and Rosenberg, A. Galois theory and Galois cohomology of commutative rings. Mem. Amer. Math. Soc. 52 (1965), 15–33.Google Scholar
[8] Chu, H., Hu, S. J., Kang, M. C. and Zhang, J. Groups with essential dimension one. Asian J. Math. 12 (2) (2008), 177–191.CrossRefGoogle Scholar
[9] Benson, D. J.. Polynomial Invariants of Finite Groups (Cambridge University Press, 1993).CrossRefGoogle Scholar
[10] Costa, D. L. Retracts of polynomial rings. J. Algebra 44 (1975), 492–502.Google Scholar
[11] Duncan, A. and Reichstein, Z. Versality of algebraic group actions and rational points on twisted varieties with an appendix containing a letter from J.–P. Serre. J. Algebraic Geom. 3 (November 2015), 499–530.CrossRefGoogle Scholar
[12] Eakin, P. A note on finite dimensional subrings of polynomial rings. Proc. Amer. Math. Soc. 31 (1) (1972), 75–80.CrossRefGoogle Scholar
[13] Fleischmann, P. and Woodcock, C. F. Non-linear group actions with polynomial invariant rings and a structure theorem for modular Galois extensions. Proc. London Math. Soc. 103 (5) (November 2011), 826–846.Google Scholar
[14] Fleischmann, P. and Woodcock, C. F. Universal Galois algebras and cohomology of p-groups. J. Pure Appl. Alg. 217 (3) (2013), 530–545.Google Scholar
[15] Fleischmann, P. and Woodcock, C. F. Modular group actions on algebras and p-local Galois extensions for finite groups. J. Alg. 442 (2015), 316–353.CrossRefGoogle Scholar
[16] Gupta, N. On the cancellation problem for the affine space $\mathbb{A}$3 in characteristic p. arXiv:1208.0483v2 (2013), pages 1–9.Google Scholar
[17] Jensen, C. U., Ledet, A. and Yui, N. Generic Polynomials. (Cambridge University Press, 2002).Google Scholar
[18] Karpenko, N. A. and Merkurjev, A. S. Essential dimension of finite p-groups. Invent. Math. 172 (3) (2008), 491–508.Google Scholar
[19] Kraft, H., Lötscher, R. and Schwarz, G. W. Compression of finnite group actions and covariant dimension II. J. Algebra 322 (2009), 94–107.CrossRefGoogle Scholar
[20] Kraft, H. and Schwarz, G. W. Compression of finnite group actions and covariant dimension. J. Algebra 313 (2007), 268–291.Google Scholar
[21] Ledet, A. Finite groups of essential dimension one. J. Algebra 311 (2007), 31–37.CrossRefGoogle Scholar
[22] Ledet, A. On the essential dimension of p-groups. In Galois theory and modular forms. Dev. Math. Vo. 11 (Kluwer, 2003), pages 159–172.Google Scholar
[23] Lorenz, M.. Multiplicative Invariant Theory (Springer, 2005).Google Scholar
[24] Popov, V. L.. Sections in Invariant Theory (Scand. Univ. Press, Oslo, 1994).Google Scholar
[25] Reichstein, Z. On the notion of essential dimension for algebraic groups. Transform. Groups 5 (2000), 265–304.Google Scholar
[26] Serre, J. P. Cohomological invariants, Witt invariants and trace forms. In Cohomological invariants in Galois cohomology (Amer. Math. Soc., 2003), pages 1–100.Google Scholar
[27] Serre, J.-P. How to use finite fields for problems concerning infinite fields. arXiv:0903.0517v2 (2009), pages 1–12.Google Scholar
[28] Smith, L. Polynomial Invariants of Finite Groups (A. K. Peters, 1995).Google Scholar
[29] Shpilrain, V. and Yu, J. T. Polynomial retracts and the Jacobian conjecture. Trans. Amer. Math. Soc. 352 (1) (1999), 477–484.Google Scholar