Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T14:36:57.084Z Has data issue: false hasContentIssue false
  • English
  • Français

The foundations of a generalization of gravitation theory

Published online by Cambridge University Press:  24 October 2008

John Moffat
John Moffat
Affiliation:
Trinity CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. Introduction. Among the more notable attempts to derive a generalization of Einstein's gravitational theory is the recent one of Einstein and Schrodinger ((1)–(8)). This was formulated by dropping the symmetry of the fundamental tensor gμν and the components 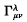of the affine connexion. The most serious defect of these non-symmetric theories is that the field equations, in their original form, do not determine the motion of electrically charged particles in an electromagnetic field, as has been proved by Infeld(9), Callaway (10) and Bonnor (n). Together with the lack of an energy-momentum tensor and a geometric description of the paths of charged particles, this seems to indicate that the concept of motion is missing in this type of theory. It is clear that one of the most important results which should follow from a generalization of Einstein's gravitational theory is the correct equations of motion of charged particles in an electromagnetic field.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 53 , Issue 2 , April 1957 , pp. 473 - 488
Copyright
Copyright © Cambridge Philosophical Society 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Einstein, A.The meaning of relativity, 4th ed. (Princeton, 1950), pp. 133–65.Google Scholar
(2)Schrödinger, E.Proc. R. Irish Acad. A, 51 (1947), 163–71 and 265–76.Google Scholar
(3)Schrödinger, E.Proc. R. Irish Acad. A, 52 (1948), 1.Google Scholar
(4)Schrödinger, E.Space time structure (Cambridge, 1954).Google Scholar
(5)Hlavaty, V. J.Rational Mech. Anal. 2 (1953), 523.Google Scholar
(6)Hlavaty, V. J.Rational Mech. Anal. 3 (1954), 103–46 and 147–79.Google Scholar
(7)Hlavaty, V.Rend. Univ. Pol. Torino, 13 (1954), 1.Google Scholar
(8)Einstein, A.Canad. J. Math. 21 (1950), 120.Google Scholar
(9)Infeld, L.Acta Phys. Polon. 10 (1951), 284.Google Scholar
(10)Callaway, J.Phys. Rev. 92 (1954), 1567.Google Scholar
(11)Bonnor, W. B.Proc. Roy. Soc. A, 226 (1954), 366.Google Scholar
(12)Einstein, A., Infeld, L. and Hoffmann, B.Ann. Math., Princeton, 39 (1938), 66.Google Scholar
(13)Einstein, A. and Infeld, L.Ann. Math., Princeton, 41 (1940), 797.Google Scholar
(14)Einstein, A. and Infeld, L.Canad. J. Math. 1 (1949), 209.Google Scholar
(15)Scheidegger, A. E.Rev. Mod. Phys. 25 (1953), 451.Google Scholar
(16)Fock, W. A.J. Exp. Theor. Phys. 7 (1939), 81.Google Scholar
(17)Infeld, L.Acta Phys. Polon. 13 (1954), 187.Google Scholar
(18)Moffat, J.Proc. Camb. Phil. Soc. 52 (1956), 623.CrossRefGoogle Scholar
(19)Einstein, A. and Rosen, N.J. Franklin Inst. 223 (1954), 43.Google Scholar
(20)Wentzel, G.Quantum theory of fields (New York, 1949).Google Scholar
(21)Infeld, L. and Plebanski, J.Bull. Acad. Pol. Sci. (4), 10 (1956), 687.Google Scholar