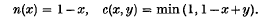Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T14:03:27.079Z Has data issue: false hasContentIssue false
  • English
  • Français

A formalization of an ℵ0-valued propositional calculus

Published online by Cambridge University Press:  24 October 2008

Alan Rose
Alan Rose
Affiliation:
The UniversityNottingham
Get access Rights & Permissions [Opens in a new window]

Extract

In 1930 Łukasiewicz (3) developed an ℵ0-valued prepositional calculus with two primitives called implication and negation. The truth-values were all rational numbers satisfying 0 ≤ x ≤ 1, 1 being the designated truth-value. If the truth-values of P, Q, NP, CPQ are x, y, n(x), c(x, y) respectively, then

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 49 , Issue 3 , July 1953 , pp. 367 - 376
Copyright
Copyright © Cambridge Philosophical Society 1953

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Church, Alonzo. Introduction to mathematical logic (Ann. Math. Stud., Princeton, 1944).Google Scholar
(2)Henkin, Leon. The completeness of the first-order functional calculus. J. symbolic Logic, 14 (1949), 159–66.CrossRefGoogle Scholar
(3)Łukasiewicz, Jan and Tarski, Alfred. Untersuchungen über den Aussagenkalkül. C. R. Soc. Sci. Varsovie (3), 23 (1930), 30–50.Google Scholar
(4)Rosser, J. B. and Turquette, A. R.Axiom schemes for m-valued prepositional calculi. J. symbolic Logic, 10 (1945), 61–82.CrossRefGoogle Scholar
(5)Rosser, J. B. and Turquette, A. R.Axiom schemes for m-valued functional calculi of the first order. J. symbolic Logic, 13 (1948), 177–92.CrossRefGoogle Scholar
Rosser, J. B. and Turquette, A. R.Axiom schemes for m-valued functional calculi of the first order. J. symbolic Logic, 16 (1951), 22–34.CrossRefGoogle Scholar