Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T07:32:54.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Flexural problems of circular ring plates and sectorial plates. II

Published online by Cambridge University Press:  24 October 2008

W. A. Bassali  and
M. A. Gorgui
W. A. Bassali
Affiliation:
Faculty of ScienceUniversity of AlexandriaAlexandria, Egypt
Get access Rights & Permissions [Opens in a new window]

Abstract

In a previous paper solutions have been derived for the deflexion of a circular annular plate under various combinations of boundary conditions and subject to certain line loadings spread along the circumference of a concentric circle. These solutions, which were used in the analysis of circular ring plates and sectorial plates acted upon by a concentrated load or a concentrated couple at any point, are utilized in this paper to obtain solutions appropriate to lateral loadings of the type 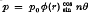distributed over the entire circular ring plate. Solutions corresponding to the case φ(r) = rm are then explicitly found, and the principle of superposition can be applied to get the solution when the load on the annulus can be expanded into a Laurent-Fourierseries in the polar coordinates r, θ. The method of images is used to deduce solutions for an isotropic plate bounded by two arcs of concentric circles and two radii, and loaded by the normal pressure p = p0rm when the plate is simply supported along the straight edges and is subject to various conditions along the circular edges.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 56 , Issue 4 , October 1960 , pp. 414 - 424
Copyright
Copyright © Cambridge Philosophical Society 1960

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bassali, W. A. and Dawoud, R. H.Proc. Math. Phys. Soc. Egypt, 21 (1957), 1.Google Scholar
(2)Bassali, W. A. and Dawoud, R. H.J. Appl. Mech. 25 (1958), 37.CrossRefGoogle Scholar
(3)Bassali, W. A. and Gorgui, M. A.Proc. Camb. Phil. Soc. 56 (1960), 75.CrossRefGoogle Scholar
(4)Carrier, G. F.J. Appl. Mech. 11 (1944), 134.CrossRefGoogle Scholar
(5)Conte, S. D.Quart. Appl. Math. 9 (1952), 435.CrossRefGoogle Scholar
(6)Eagle, H. A. and Ross, A. L.J. Appl. Mech. 25 (1958), 157.CrossRefGoogle Scholar
(7)Flügge, W.Bauingenieur, 10 (1929), 221.Google Scholar
(8)Galerkin, B. G.Elastic thin plates. (Moscow, 1933.)Google Scholar
(9)Georgian, J. C.J. Appl. Mech. 24 (1957), 306.CrossRefGoogle Scholar
(10)Ghose, S.Bull. Calcutta Math. Soc. 16 (1925), 117.Google Scholar
(11)Nadai, A. Z.Ver. deut. Ing. 59 (1915), 169.Google Scholar
(12)Saito, A., Kawakami, O. and Saito, J.Proc. 5th Jap. Nat. Gongr. Appl. Mech. (1955), 99.Google Scholar
(13)Sekiya, T. and Wada, Y.Proc. 6th Jap. Nat. Congr. Appl. Mech. (1956), 145.Google Scholar
(14)Sen, B.Phil. Mag. (7), 20 (1935), 1158.CrossRefGoogle Scholar
(15)Timoshenko, S.Theory of plates and shells. (New York, 1940).Google Scholar
(16)Yu, Y. Y.Proc. 9th internat. Congr. Appl. Mech. (Brussels, 1956), 378.Google Scholar