Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-29T18:58:55.888Z Has data issue: false hasContentIssue false
  • English
  • Français

FK spaces which include strongly summable sequences

Published online by Cambridge University Press:  24 October 2008

I. J. Maddox
I. J. Maddox
Affiliation:
Queen's University of Belfast
Get access Rights & Permissions [Opens in a new window]

Extract

The following interesting result on strongly summable sequences is due to Kuttner (2).

Theorem 1. Let 0 < p < 1. Then given any Toeplitz matrix A there is a sequence summable wp which is not summable A.

As usual, for 0 < p < ∞, we denote by wp the space of strongly summable sequences with index p. Thus x = (xk) ∈ wp if and only if there is a number l such that

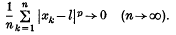
Strongly summable sequences arise in the theory of Fourier series, see e.g. (8), Chapter X, in Ergodic theory, see e.g. (1), as well as in summability theory.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 93 , Issue 1 , January 1983 , pp. 131 - 134
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Halmos, P. R.Lectures on Ergodic Theory (Chelsea, New York, 1956).Google Scholar
(2)Kuttner, B.Note on strong summability. J. London Math. Soc. 21 (1946), 118–122.Google Scholar
(3)Lascarides, C. G. and Maddox, I. J.Matrix transformations between some classes of sequences. Proc. Cambridge Phil. Soc. 68 (1970), 99–104.CrossRefGoogle Scholar
(4)Maddox, I. J.On Kuttner's theorem. J. London Math. Soc. 43 (1968), 285–290.CrossRefGoogle Scholar
(5)Snyder, A. K. and Wilansky, A.Inclusion theorems and semiconservative FK spaces. Rocky Mountain J. Math. 2 (1972), 595–603.Google Scholar
(6)Thorpe, B.An extension of Kuttner's theorem. Bull. London Math. Soc. 13 (1981), 301–302.Google Scholar
(7)Zeller, K.Allgemeine Eigenschaften von Limitierungsverfahren. Math. Zeit. 53 (1951), 463–487.Google Scholar
(8)Zygmund, A.Trigonometrical Series. (Dover Publications, 1955).Google Scholar