Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T01:43:06.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite group schemes of p-rank ≤ 1

Published online by Cambridge University Press:  27 November 2017

HAO CHANG  and
ROLF FARNSTEINER
HAO CHANG
Affiliation:
Mathematisches Seminar, Christian–Albrechts–Universität zu Kiel, Ludewig–Meyn–Str. 4, 24098 Kiel, Germany. Current address: School of Mathematics and Statistics, Central China Normal University, 430079 Wuhan, People's Republic of China. e-mail: [email protected]
ROLF FARNSTEINER
Affiliation:
Mathematisches Seminar, Christian–Albrechts–Universität zu Kiel, Ludewig–Meyn–Str. 4, 24098 Kiel, Germany. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 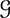be a finite group scheme over an algebraically closed field k of characteristic char(k) = p ≥ 3. In generalisation of the familiar notion from the modular representation theory of finite groups, we define the p-rank rkp(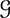) of 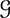and determine the structure of those group schemes of p-rank 1, whose linearly reductive radical is trivial. The most difficult case concerns infinitesimal groups of height 1, which correspond to restricted Lie algebras. Our results show that group schemes of p-rank ≤ 1 are closely related to those being of finite or domestic representation type.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 166 , Issue 2 , March 2019 , pp. 297 - 323
Copyright
Copyright © Cambridge Philosophical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Alperin, J. and Evens, L. Representations, resolutions and Quillen's dimension theorem. J. Pure Appl. Algebra 22 (1981), 1–9.Google Scholar
[2] Benkart, G. and Osborn, J. Representations of rank 1 Lie algebras of characteristic p. Lecture Notes in Math. 933 (1982), 1–37.Google Scholar
[3] Block, R. On the extensions of Lie algebras. Canad. J. Math. 20 (1968), 1439–1450.Google Scholar
[4] Brauer, R. On finite groups with cyclic Sylow subgroups, I. J. Algebra 40 (1976), 556–584.Google Scholar
[5] Brauer, R. On finite groups with cyclic Sylow subgroups, II. J. Algebra 58 (1979), 291–318.Google Scholar
[6] Carlson, J., Friedlander, E. and Pevtsova, J. Elementary subalgebras of Lie algebras. J. Algebra 442 (2015), 155–189.Google Scholar
[7] Cartan, H. and Eilenberg, S.. Homological Algebra. Princeton Math. Ser. 19, (Princeton University Press, 1956).Google Scholar
[8] Chang, H. Varieties of elementary Lie algebras. PhD. thesis. University of Kiel (2016).Google Scholar
[9] Chang, H. A note on the rank of a restricted Lie algebra. arXiv: 1609.01446 [math. RT]Google Scholar
[10] Chwe, B. On the commutativity of restricted Lie algebras. Proc. Amer. Math. Soc. 16 (1965), 547.Google Scholar
[11] Demazure, M. and Gabriel, P.. Groupes Algébriques (North–Holland, 1970).Google Scholar
[12] Demushkin, S. Cartan subalgebras of simple Lie-p-algebras W n and S n. Siberian Math. J. 11 (1970), 233–245.Google Scholar
[13] Demushkin, S. Cartan subalgebras of simple non-classical Lie-p-algebras. Math. USSR Izvestija 6 (1972), 905–924.Google Scholar
[14] Farnsteiner, R. Central extensions and invariant forms of graded Lie algebras. Algebras, Groups, Geom. 3 (1986), 431–455.Google Scholar
[15] Farnsteiner, R. Derivations and central extensions of finitely generated graded Lie algebras. J. Algebra 118 (1988), 33–45.Google Scholar
[16] Farnsteiner, R. Periodicity and representation type of modular Lie algebras. J. Reine Angew. Math. 464 (1995), 47–65.Google Scholar
[17] Farnsteiner, R. Varieties of tori and Cartan subalgebras of restricted Lie algebras. Trans. Amer. Math. Soc. 356 (2004), 4181–4236.Google Scholar
[18] Farnsteiner, R. Polyhedral groups, McKay quivers, and the finite algebraic groups with tame principal blocks. Invent. Math. 166 (2006), 27–94.Google Scholar
[19] Farnsteiner, R. Combinatorial and geometric aspects of the representation theory of finite group schemes. In Lie Theory and Representation Theory. Surveys of Modern Math. 2 (2010), 47–149.Google Scholar
[20] Farnsteiner, R. Extensions of tame algebras and finite group schemes of domestic representation type. Forum Math. 27 (2015), 1071-1100.Google Scholar
[21] Farnsteiner, R. Representations of finite group schemes and morphisms of projective varieties. Proc. London Math. Soc. 114 (2017), 433–475.Google Scholar
[22] Farnsteiner, R., Röhrle, G. and Voigt, D. Infinitesimal unipotent group schemes of complexity 1. Colloq. Math. 89 (2001), 179–192.Google Scholar
[23] Farnsteiner, R. and Voigt, D. Modules of solvable infinitesimal groups and the structure of representation-finite cocommutative Hopf algebras. Math. Proc. Camb. Phil. Soc. 127 (1999), 441–459.Google Scholar
[24] Farnsteiner, R. and Voigt, D. On cocommutative Hopf algebras of finite representation type. Adv. Math. 155 (2000), 1–22.Google Scholar
[25] Farnsteiner, R. and Voigt, D. On infinitesimal groups of tame representation type. Math. Z. 244 (2003), 479–513.Google Scholar
[26] Friedlander, E. and Parshall, B. Support varieties for restricted Lie algebras. Invent. Math. 86 (1986), 553–562.Google Scholar
[27] Friedlander, E. and Parshall, B. Geometry of p-unipotent Lie algebras. J. Algebra 109 (1987), 25–45.Google Scholar
[28] Friedlander, E. and Pevtsova, J. Representation-theoretic support spaces of finite group schemes. Amer. J. Math. 127 (2005), 379–420. Erratum: Amer. J. Math. 128 (2006), 1067–1068.Google Scholar
[29] Hartshorne, R. Algebraic Geometry. Grad. Texts in Math. 52 (Springer–Verlag, 1977).Google Scholar
[30] Higman, D. Indecomposable representations of characteristic p. Duke J. Math. 21 (1954), 377–381.Google Scholar
[31] Hilton, P. and Stammbach, U. A Course in Homological Algebra. Grad. Texts in Math. 4 (Springer–Verlag, 1970).Google Scholar
[32] Jantzen, J.. Representations of Algebraic Groups. Math. Surv. Monogr. 107 (American Math. Society, Providence, 2006).Google Scholar
[33] Pollack, R. Restricted Lie algebras of bounded type. Bull. Amer. Math. Soc. 74 (1968), 326–331.Google Scholar
[34] Hochschild, G. Representations of restricted Lie algebras of characteristic p. Proc. Amer. Math. Soc. 5 (1954), 603–605.Google Scholar
[35] Premet, A. Green ring for simple three-dimensional Lie-p-algebra. Soviet Mathematics (Iz. VUZ) 35 (1991), 51–60.Google Scholar
[36] Ringel, C. Tame algebras. In Representation Theory I (Ottawa 1979). Lecture Notes in Math. 831 (1980), 137–287.Google Scholar
[37] Ringel, C. The elementary 3-Kronecker modules. arXiv:1612.09141 [math. RT]Google Scholar
[38] Strade, H. and Farnsteiner, R.. Modular Lie Algebras and their Representations. Pure Appl. Math. 116 (Marcel Dekker, 1988).Google Scholar
[39] Suslin, A., Friedlander, E. and Bendel, C. Infinitesimal one-parameter subgroups and cohomology. J. Amer. Math. Soc. 10 (1997), 693–728.Google Scholar
[40] Suslin, A., Friedlander, E. and Bendel, C. Support varieties for infinitesimal group schemes. J. Amer. Math. Soc. 10 (1997), 729–759.Google Scholar
[41] Voigt, D.. Induzierte Darstellungen in der Theorie der endlichen, algebraischen Gruppen. Lecture Notes in Math. 592 (Springer–Verlag, 1977).Google Scholar
[42] Waterhouse, W.. Introduction to Affine Group Schemes. Graduate Texts in Math. 66 (Springer–Verlag, 1979).Google Scholar