Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T14:59:09.863Z Has data issue: false hasContentIssue false
  • English
  • Français

Field theories with high derivatives

Published online by Cambridge University Press:  24 October 2008

T. S. Chang
T. S. Chang
Affiliation:
Fitzwilliam HouseCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

The relativistic field theories of elementary particles are extended to cases where the field equations are derived from Lagrangians containing all derivatives of the field quantities. Expressions for the current, the energy-momentum tensor, the angular-momentum tensor, and the symmetrized energy-momentum tensor are given. When the field interacts with an electromagnetic field, we introduce a subtraction procedure, by which all the above expressions are made gauge-invariant. The Hamiltonian formulation of the equations of motion in a gauge-invariant form is also given.

After considering the Lagrangian L as a scalar in a general relativity transformation and thus a function of gμν and their derivatives, the functional derivative of

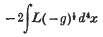
with respect to gμν (x) at a point where the space time is flat is worked out. It is shown that this differs from the symmetrized energy-momentum tensor given in the above sections by a term which vanishes when certain operators Sij are antisymmetrical or when the Lagrangian contains the first derivatives of the field quantities only and whose divergence to either μ or ν vanishes.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 44 , Issue 1 , January 1948 , pp. 76 - 86
Copyright
Copyright © Cambridge Philosophical Society 1948

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† Pauli, W., Rev. Mod. Phys. 13 (1941), 203.CrossRefGoogle Scholar

‡ Belinfante, F. J., Physica, 6 (1939), 887;CrossRefGoogle Scholar 7 (1940), 305. Rosenfeld, L., Mem. Acad. Roy. Belg. 6 (1940), 30.Google Scholar

§ Eddington proved that the divergence of (− g)−½ times the functional derivative of any invariant integral with respect to g μν is zero. See Eddington, , The mathematical theory of relativity (1923), p. 140.Google Scholar

† See Eddington, loc. cit. p. 138, where it is proved that

‡ The casting of equations obtained by varying a Lagrangian containing all derivatives of the field quantities into the canonical form has been given by the author (Proc. Cambridge Phil. Soc. 42 (1946), 132).Google Scholar

§ See for example, Bhabha, H. J., Proc. Indian Acad. Sci. A, 21 (1945), 241.Google Scholar

† Pauli, W., loc. cit.

‡ Chang T. S., loc. cit.