Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-04T21:29:15.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Fatou–Zygmund sets

Published online by Cambridge University Press:  24 October 2008

Kenneth A. Ross
Kenneth A. Ross
Affiliation:
University of Oregon
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let G be a compact Abelian group with character group X. Let 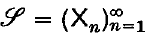be an increasing sequence of finite symmetric subsets of X, and consider a symmetric subset P of 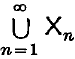. For any Hermitian complex-valued function u on P, we write snu for the real-valued trigonometric polynomial 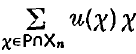. Edwards, Hewitt and Ross(4) investigated the following property for a non-void measurable subset W of G satisfying W ⊂ (int W)−:

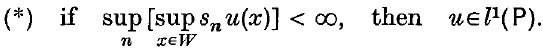
The validity of this implication was shown to be independent of the choice of 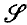. Accordingly, if (*) holds, P is called an FZ(W)-set. If P is an FZ(W)-set for all W, then P is termed a full FZ-set or full Fatou-Zygmund set. In this paper, we characterize the full FZ-sets as FZ(G)-sets satisfying a certain algebraic condition. In particular, we show that if G is connected, then a symmetric subset of X is an FZ(G)-set if and only if it is a full FZ-set. Some of the techniques are adaptations of those of Mme Déchamps-Gondim(1), (2). The class of full FZ-sets is not always closed under the operation of finite unions; this contrasts with the situation for Sidon sets and for FZ(G)-sets.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 73 , Issue 1 , January 1973 , pp. 57 - 65
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Déchams-Gondim, M.Compacts associés à un ensemble de Sidon. C.R. Acad. Sci. Paris, Sér. A, 271 (1970), 590–592.Google Scholar
(2)Décamps-Gondim, M.Ensembles de Sidon topologiques. Ann. Inst. Fourier (Grenoble) 22, 3 (1972).Google Scholar
(3)Drury, S. W.Sur les ensembles de Sidon. C.R. Acad. Sci. Paris, Sér. A, 271 (1970), 162–163.Google Scholar
(4)Edwards, R. E., Hewitt, E. and Ross, K. A.Lacunarity for compact groups. III. Studia Math. 44 (1972), 19–66.CrossRefGoogle Scholar
(5)Hewitt, E. and Ross, K. A.Abstract harmonic analysis, 2 vols. (Berlin-Heidelberg-New York: Springer-Verlag, 1963, 1970.)Google Scholar