Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Powell, Wayne B.
1989.
Ordered Algebraic Structures.
p.
11.
Kopytov, V. M.
and
Medvedev, N. Ya.
1996.
Ordered Groups and Infinite Permutation Groups.
p.
1.
Nola, A. Di
Dvurečenskij, A.
and
Tsinakis, C.
2008.
Perfect GMV-Algebras.
Communications in Algebra,
Vol. 36,
Issue. 4,
p.
1221.
Metcalfe, George
Montagna, Franco
and
Tsinakis, Constantine
2014.
Amalgamation and interpolation in ordered algebras.
Journal of Algebra,
Vol. 402,
Issue. ,
p.
21.
Gil-Férez, José
Ledda, Antonio
and
Tsinakis, Constantine
2015.
The Failure of The Amalgamation Property for Semilinear Varieties of Residuated Lattices.
Mathematica Slovaca,
Vol. 65,
Issue. 4,
p.
817.


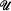 satisfies the
satisfies the 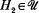 and embeddings τ
and embeddings τ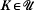 and embeddings σ
and embeddings σ