Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T22:05:24.208Z Has data issue: false hasContentIssue false
  • English
  • Français

The factorisation property of l∞(Xk)

Part of: Normed linear spaces and Banach spaces; Banach lattices General theory of linear operators Spaces and algebras of analytic functions

Published online by Cambridge University Press:  10 December 2020

RICHARD LECHNER ,
PAVLOS MOTAKIS ,
PAUL F.X. MÜLLER  and
THOMAS SCHLUMPRECHT
RICHARD LECHNER
Affiliation:
Institute of Analysis, Johannes Kepler University Linz, Altenberger Strasse 69, A-4040 Linz, Austria. e-mail: [email protected]
PAVLOS MOTAKIS
Affiliation:
Department of Mathematics and Statistics, York University, 4700 Keele Street, Toronto, Ontario, M3J 1P3, Canada. e-mail: [email protected]
PAUL F.X. MÜLLER
Affiliation:
Institute of Analysis, Johannes Kepler University Linz, Altenberger Strasse 69, A-4040 Linz, Austria. e-mail: [email protected]
THOMAS SCHLUMPRECHT
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX77843-3368, U.S.A. and Faculty of Electrical Engineering, Czech Technical University in Prague, Zikova 4, 16627, Prague, Czech Republic. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider the following problem: let Xk, be a Banach space with a normalised basis (e(k, j))j, whose biorthogonals are denoted by 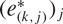${(e_{(k,j)}^*)_j}$ , for 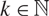$k\in\N$ , let 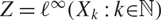$Z=\ell^\infty(X_k:k\kin\N)$ be their l∞-sum, and let 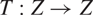$T:Z\to Z$ be a bounded linear operator with a large diagonal, i.e.,

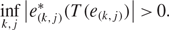$$\begin{align*}\inf_{k,j} \big|e^*_{(k,j)}(T(e_{(k,j)})\big|>0.\end{align*}$$
Under which condition does the identity on Z factor through T? The purpose of this paper is to formulate general conditions for which the answer is positive.

MSC classification

Primary: 46B25: Classical Banach spaces in the general theory 46B26: Nonseparable Banach spaces 47A68: Factorization theory (including Wiener-Hopf and spectral factorizations) 30H10: Hardy spaces
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 2 , September 2021 , pp. 421 - 448
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Cambridge Philosophical Society 2020

Footnotes

†

Supported by the Austrian Science Foundation (FWF) under Grant Number Pr.Nr. P28352, P32728 and by the 2019 workshop in Analysis and Probability at Texas A&M University.

‡

Supported by the National Science Foundation under Grant Number DMS-1912897.

§

Supported by the Austrian Science Foundation (FWF) under Grant Number Pr.Nr. P28352 and by the 2019 workshop in Analysis and Probability at Texas A&M University.

‖

Supported by the National Science Foundation under Grant Numbers DMS-1464713 and DMS-1711076.

References

REFERENCES

Blower, G.. The Banach space B(l 2) is primary. Bull. London Math. Soc. 22(2) (1990), 176–182.CrossRefGoogle Scholar
Bourgain, J.. On the primarity of H ∞-spaces. Israel J. Math. 45(4) (1983), 329–336.CrossRefGoogle Scholar
Bourgain, J.. Vector-valued singular integrals and the H 1-BMO duality. In Probability theory and harmonic analysis (Cleveland, Ohio, 1983), volume 98 of Monogr. Textbooks Pure Appl. Math. Dekker, New York, 1986, 1–19.Google Scholar
Capon, M.. Primarité de certains espaces de Banach. Proc. London Math. Soc. (3), 45(1) (1982), 113–130.CrossRefGoogle Scholar
Capon, M.. Primarité de L p(L r), 1 < p, r < ∞. Israel J. Math. 42(1-2) (1982), 87–98.CrossRefGoogle Scholar
Haydon, R., Odell, E., and Schlumprecht, T.. Small subspaces of Lp. Ann. of Math. (2), 173(1) (2011), 169–209.CrossRefGoogle Scholar
James, R. C.. Bases and reflexivity of Banach spaces. Ann. of Math. (2), 52 (1950), 518–527.Google Scholar
Johnson, W. B.. A complementary universal conjugate Banach space and its relation to the approximation problem. Israel J. Math. 13 (1973), 301–310.CrossRefGoogle Scholar
Kahane, J.-P.. Some random series of functions, Camb. Stud. Adv. Math. vol. 5 (Cambridge University Press, Cambridge, second edition, 1985).Google Scholar
Laustsen, N. J., Lechner, R., and Müller, P. F. X.. Factorization of the identity through operators with large diagonal. J. Funct. Anal. 275(11) (2018), 3169–3207.CrossRefGoogle Scholar
Lechner, R.. Factorization in mixed norm Hardy and BMO spaces. Studia Math. 242(3) (2018), 231–265.CrossRefGoogle Scholar
Lechner, R.. Subsymmetric weak Schauder bases and factorization of the identity. Studia Math. 248(3) (2019), 295–319.CrossRefGoogle Scholar
Lechner, R., Motakis, P., Müller, P. F. X., and Th. Schlumprecht. Strategically reproducible bases and the factorization property. Israel J. Math. 238(1) (2020), 13–60.Google Scholar
Lindenstrauss, J.. On complemented subspaces of m . Israel J. Math. 5 (1967), 153–156.CrossRefGoogle Scholar
Lindenstrauss, J. and Tzafriri, L.. Classical Banach spaces. I (Springer-Verlag, Berlin-New York 1977). Sequence spaces, Ergeb. d. Math. Grenzgeb. vol. 92.Google Scholar
Maurey, B., Milman, V. D., and Tomczak-Jaegermann, N.. Asymptotic infinite-dimensional theory of Banach spaces. In Geometric aspects of functional analysis (Israel, 1992–1994), volume 77 of Oper. Theory Adv. Appl. vol 77 (Birkhäuser, Basel, 1995), pages 149–175.Google Scholar
Müller, P. F. X.. On projections in H 1 and BMO. Studia Math. 89(2) (1988), 145–158.CrossRefGoogle Scholar
Müller, P. F. X.. Isomorphisms between H 1 spaces, volume 66 of Instytut Matematyczny Polskiej Akademii Nauk. Monografie Matematyczne (New Series) [Mathematics Institute of the Polish Academy of Sciences. Mathematical Monographs (New Series)]. (Birkhäuser Verlag, Basel, 2005).Google Scholar
Müller, P. F. X.. Two remarks on primary spaces. Math. Proc. Camb. Phil. Soc. 153(3) (2012), 505–523.CrossRefGoogle Scholar
Müller, P. F. X. and Schechtman, G.. Several results concerning unconditionality in vector valued L p and $H^1(\mathcal{F}_n)$ spaces. Illinois J. Math. 35(2) (1991), 220–233.CrossRefGoogle Scholar
Odell, E. and Schlumprecht, T.. Trees and branches in Banach spaces. Trans. Amer. Math. Soc. 354(10) (2002), 4085–4108.CrossRefGoogle Scholar
Odell, E. and Schlumprecht, T.. A universal reflexive space for the class of uniformly convex Banach spaces. Math. Ann. 335(4) (2006), 901–916.CrossRefGoogle Scholar
Odell, E., Schlumprecht, T., and Zsák, A.. A new infinite game in Banach spaces with applications. In Banach Spaces and their Applications in Analysis, (Walter de Gruyter, Berlin, 2007), pages 147–182.Google Scholar
Pisier, G.. Martingales in Banach spaces. Camb. Stud. Adv. Math. (Cambridge University Press, Cambridge, 2016).Google Scholar
Rosendal, C.. Infinite asymptotic games. Ann. Inst. Fourier (Grenoble), 59(4) (2009), 1359–1384.CrossRefGoogle Scholar
Wark, H. M.. The l ∞ direct sum of L p (1 < p < ∞) is primary. J. Lond. Math. Soc. (2), 75(1) (2007), 176–186.CrossRefGoogle Scholar
Wojtaszczyk, P.. Banach spaces for analysts. Camb. Stud. Adv. Math. vol. 25 (Cambridge University Press, Cambridge, 1991).Google Scholar