No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 24 October 2008
The lemma I propose to discuss may be stated as follows;
If ξ, η, ζ are three quantities whose sum is zero and λ, μ, ν three positive integers (≤n) satisfying the condition
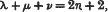
then any polynomial of order n in ξ, η, ζ can be expressed in the form
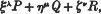
where P, Q, R are polynomials of orders n − λ, n − μ, n − ν.
* Math. Ann. Bd XXXI, p. 444Google Scholar. Cf. Algebra of Invariants, p. 62. The case of n = 1 is trivial, exceptional, and ignored throughout.Google Scholar
† The number is: g(n−λ)+g(n−μ)+g(n−ν)+g(n−ρ)Google Scholar
* This as usual means
or
The word apolar is frequently used in the same sense.
† There is a trifling modification for two variables, the case which gives Stroh's lemma, because the principle of duality is unnecessary in one dimension. Cf. Bertini, , Geometria projettiva degli iperspazi (1923), p. 260. I return to the point in §6.Google Scholar
* Proc. Lond. Math. Soc. (2) I, pp. 345–350 (1903).Google Scholar The thesis there was to prove that expression is possible with each exponent equal to or greater than n/2 and this of course follows from the particular cases. It follows from the general theorem of §1, since one of the integers
must be divisible by 4.
* Cf. Algebra of Invariants, p. 375.Google Scholar