Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-29T22:30:01.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Expected number of real zeros for random orthogonal polynomials

Published online by Cambridge University Press:  27 September 2016

DORON S. LUBINSKY ,
IGOR E. PRITSKER  and
XIAOJU XIE
DORON S. LUBINSKY
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332, U.S.A. e-mail: [email protected]
IGOR E. PRITSKER
Affiliation:
Department of Mathematics, Oklahoma State University, Stillwater, OK 74078, U.S.A. e-mails: [email protected]; [email protected]
XIAOJU XIE
Affiliation:
Department of Mathematics, Oklahoma State University, Stillwater, OK 74078, U.S.A. e-mails: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the expected number of real zeros for random linear combinations of orthogonal polynomials. It is well known that Kac polynomials, spanned by monomials with i.i.d. Gaussian coefficients, have only (2/π + o(1))logn expected real zeros in terms of the degree n. If the basis is given by the orthonormal polynomials associated with a compactly supported Borel measure on the real line, or associated with a Freud weight defined on the whole real line, then random linear combinations have 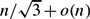$n/\sqrt{3} + o(n)$ expected real zeros. We prove that the same asymptotic relation holds for all random orthogonal polynomials on the real line associated with a large class of weights, and give local results on the expected number of real zeros. We also show that the counting measures of properly scaled zeros of these random polynomials converge weakly to either the Ullman distribution or the arcsine distribution.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 164 , Issue 1 , January 2018 , pp. 47 - 66
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bharucha-Reid, A. T. and Sambandham, M. Random Polynomials (Academic Press, Orlando, 1986).Google Scholar
[2] Billingsley, P. Convergence of Probability Measures (John Wiley & Sons, Inc., New York, 1999).CrossRefGoogle Scholar
[3] Blatt, H.-P., Saff, E. B. and Simkani, M. Jentzsch-Szegő type theorems for the zeros of best approximants. J. London Math. Soc. 38 (1988), 307–316.CrossRefGoogle Scholar
[4] Bloch, A. and Pólya, G. On the roots of certain algebraic equations. Proc. London Math. Soc. 33 (1932), 102–114.CrossRefGoogle Scholar
[5] Bloom, T. Random polynomials and (pluri)potential theory. Ann. Polon. Math. 91 (2007), 131–141.Google Scholar
[6] Bloom, T. and Levenberg, N. Random polynomials and pluripotential-theoretic extremal functions. Potential Anal. 42 (2015), 311–334.Google Scholar
[7] Cramér, H. and Leadbetter, M. R. Stationary and Related Stochastic Processes (Wiley, New York, 1966).Google Scholar
[8] Das, M. Real zeros of a random sum of orthogonal polynomials. Proc. Amer. Math. Soc. 27 (1971), 147–153.Google Scholar
[9] Das, M. The average number of real zeros of a random trigonometric polynomial. Proc. Camb. Phil. Soc. 64 (1968), 721–729.CrossRefGoogle Scholar
[10] Das, M. and Bhatt, S. S. Real roots of random harmonic equations. Indian J. Pure Appl. Math. 13 (1982), 411–420.Google Scholar
[11] Edelman, A. and Kostlan, E. How many zeros of a random polynomial are real? Bull. Amer. Math. Soc. 32 (1995), 1–37.CrossRefGoogle Scholar
[12] Erdős, P. and Offord, A. C. On the number of real roots of a random algebraic equation. Proc. London Math. Soc. 6 (1956), 139–160.CrossRefGoogle Scholar
[13] Farahmand, K. Topics in Random Polynomials . Pitman Res. Notes Math. 393 (1998).Google Scholar
[14] Farahmand, K. Level crossings of a random orthogonal polynomial. Analysis 16 (1996), 245–253.Google Scholar
[15] Farahmand, K. On random orthogonal polynomials. J. Appl. Math. Stochastic Anal. 14 (2001), 265–274.Google Scholar
[16] Freud, G. Orthogonal Polynomials (Akademiai Kiado/Pergamon Press, Budapest, 1971).Google Scholar
[17] Gut, A. Probability: a Graduate Course (Springer, New York, 2005).Google Scholar
[18] Ibragimov, I. A. and Maslova, N. B. The average number of zeros of random polynomials. Vestnik Leningrad University 23 (1968), 171–172.Google Scholar
[19] Ibragimov, I. A. and Maslova, N. B. The mean number of real zeros of random polynomials. I. Coefficients with zero mean. Theory Probab. Appl. 16 (1971), 228–248.Google Scholar
[20] Kac, M. On the average number of real roots of a random algebraic equation. Bull. Amer. Math. Soc. 49 (1943), 314–320.Google Scholar
[21] Kac, M. On the average number of real roots of a random algebraic equation. II. Proc. London Math. Soc. 50 (1948), 390–408.CrossRefGoogle Scholar
[22] Kac, M. Nature of probability reasoning, Probability and related topics in physical sciences, Proceedings of the Summer Seminar (Boulder, Colorado 1957) vol. I (Interscience Publishers, London-New York, 1959).Google Scholar
[23] Landkof, N. S. Foundations of Modern Potential Theory (Springer-Verlag, New York-Heidelberg, 1972).Google Scholar
[24] Levin, E. and Lubinsky, D. S. Orthogonal Polynomials for Exponential Weights (Springer, New York, 2001).Google Scholar
[25] Levin, E. and Lubinsky, D. S. Applications of universality limits to zeros and reproducing kernels of orthogonal polynomials. J. Approx. Theory 150 (2008), 69–95.Google Scholar
[26] Levin, E. and Lubinsky, D. S. Universality limits for exponential weights. Constr. Approx. 29 (2009), 247–275.Google Scholar
[27] Littlewood, J. E. and Offord, A. C. On the number of real roots of a random algebraic equation. J. London Math. Soc. 13 (1938), 288–295.CrossRefGoogle Scholar
[28] Littlewood, J. E. and Offord, A. C. On the number of real roots of a random algebraic equation. II. Proc. Camb. Philos. Soc. 35 (1939), 133–148.Google Scholar
[29] Lubinsky, D. S., Pritsker, I. E., and Xie, X. Expected number of real zeros for random linear combinations of orthogonal polynomials. Proc. Amer. Math. Soc. 144 (2016), 1631–1642.Google Scholar
[30] Mhaskar, H. N. Introduction to the Theory of Weighted Polynomial Approximation (World Scientific, Singapore, 1996).Google Scholar
[31] Mhaskar, H. N. and Saff, E. B. Extremal problems for polynomials with exponential weights. Trans. Amer. Math. Soc. 285 (1984), 203–234.Google Scholar
[32] Pritsker, I. E. Zero distribution of random polynomials. J. Anal. Math., to appear. arXiv:1409.1631Google Scholar
[33] Pritsker, I. E. and Xie, X. Expected number of real zeros for random Freud orthogonal polynomials. J. Math. Anal. Appl. 429 (2015), 1258–1270.Google Scholar
[34] Ransford, T. Potential Theory in the Complex Plane (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
[35] Saff, E. B. and Totik, V. Logarithmic Potentials with External Fields (Springer, New York, 1997).Google Scholar
[36] Stevens, D. C. The average number of real zeros of a random polynomial. Comm. Pure Appl. Math. 22 (1969), 457–477.CrossRefGoogle Scholar
[37] Wang, Y. J. Bounds on the average number of real roots of a random algebraic equation. Chinese Ann. Math. Ser. A. 4 (1983), 601–605.Google Scholar
[38] Wilkins, J. E. Jr., An asymptotic expansion for the expected number of real zeros of a random polynomial. Proc. Amer. Math. Soc. 103 (1988), 1249–1258.Google Scholar
[39] Wilkins, J. E. Jr., The expected value of the number of real zeros of a random sum of Legendre polynomials. Proc. Amer. Math. Soc. 125 (1997), 1531–1536.Google Scholar