Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T14:34:49.229Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansions of Generalized Hypergeometric Functions in Series of Products of Generalized Whittaker Functions

Published online by Cambridge University Press:  24 October 2008

F. M. Ragab
F. M. Ragab
Affiliation:
Mathematical InstituteUniversity of BonnGermany Faculty of ScienceCairo UniversityU.A.R.(EGYPT)
Get access Rights & Permissions [Opens in a new window]

Extract

In a previous paper (l) in this journal L. J. Slater gave expansions of the generalized Whittaker functions 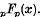. She gave this name to the generalized hypergeometric function 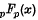in the sense that it is a generalization of the well-known Whittaker function 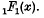. In this paper series of products of generalized Whittaker functions will be evaluated in terms of such functions or in terms of generalized hypergeometric functions pFp(x). 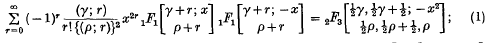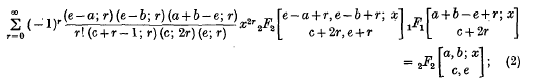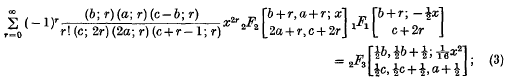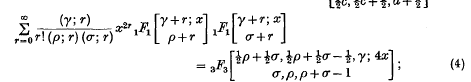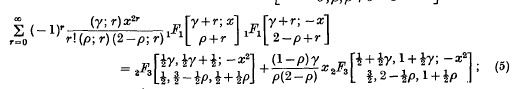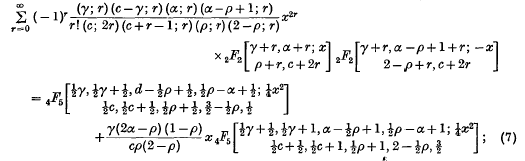These expansions are 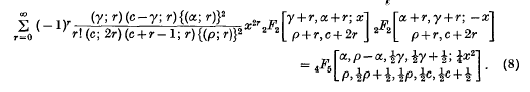These formulae will be proved in § 2 and particular cases will be given in § 3.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 2 , April 1962 , pp. 239 - 243
Copyright
Copyright © Cambridge Philosophical Society 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Slater, L. JProc. Cambridge Philos. Soc. 50 (1954), 628–631.CrossRefGoogle Scholar
(2)Saalschüutz, L. Z.Math. Phys. 35 (1890), 186–188.Google Scholar
(3)Dixon, A. CProc. London Math. Soc. (1), 35 (1902–1903), 285–289.Google Scholar
(4)Watson, G. NProc. London Math. Soc. (2), 22 (1923–1934), 163–170; 23 (1924–5), xiii–xv.Google Scholar
(5)Whipple, F. J. W.Proc. London Math. Soc. (2), 24 (1925–1926), 247–263.Google Scholar
(6)Dougall, J.Proc. Edinburgh Math. Soc. (25), (1907), 114–132.CrossRefGoogle Scholar
(7)Kummer, E. EJ. Reine Angew. Math. 15 (1836), 39–83.Google Scholar
(8)Gauss, C. FWerke, Bd 3, 123–163 and 207–229 (Göottingen, 1866).Google Scholar