Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T13:38:05.915Z Has data issue: false hasContentIssue false
  • English
  • Français

Escaping Fatou components of transcendental self-maps of the punctured plane

Part of: Complex dynamical systems Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  28 November 2019

DAVID MARTÍ-PETE
DAVID MARTÍ-PETE*
Affiliation:
Department of Mathematics, Kyoto University, Kyoto 606-8502, Japan. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the iteration of transcendental self-maps of 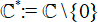$\mathcal{C}^*:\=\mathcal{C}\{0}$, that is, holomorphic functions 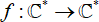$\fnof:\mathcal{C}^*:\rarr\mathcal{C}^*$ for which both zero and infinity are essential singularities. We use approximation theory to construct functions in this class with escaping Fatou components, both wandering domains and Baker domains, that accumulate to 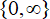$\{0},\infin$ in any possible way under iteration. We also give the first explicit examples of transcendental self-maps of 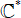$\mathcal{C}^*$ with Baker domains and with wandering domains. In doing so, we developed a sufficient condition for a function to have a simply connected escaping wandering domain. Finally, we remark that our results also provide new examples of entire functions with escaping Fatou components.

MSC classification

Primary: 37F10: Polynomials; rational maps; entire and meromorphic functions
Secondary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 170 , Issue 2 , March 2021 , pp. 265 - 289
Copyright
© Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arakelyan, N. U.. Uniform approximation on closed sets by entire functions. Izv. Akad. Nauk SSSR Ser. Mat. 28 (1964), 1187–1206.Google Scholar
Baker, I. N.. Multiply connected domains of normality in iteration theory. Math. Z. 81 (1963), 206–214.CrossRefGoogle Scholar
Baker, I. N.. An entire function which has wandering domains. J. Austral. Math. Soc. Ser. A 22 (1976), no. 2, 173–176.CrossRefGoogle Scholar
Baker, I. N.. Wandering domains in the iteration of entire functions. Proc. London Math. Soc. (3) 49 (1984), no. 3, 563–576.CrossRefGoogle Scholar
Baker, I. N.. Wandering domains for maps of the punctured plane. Ann. Acad. Sci. Fenn. Ser. A I Math. 12 (1987), no. 2, 191–198.CrossRefGoogle Scholar
Baker, I. N. and Domínguez-Soto, P.. Analytic self-maps of the punctured plane. Complex Variables Theory Appl. 37 (1998), no. 1-4, 67–91.CrossRefGoogle Scholar
Bergweiler, W.. Iteration of meromorphic functions. Bulletin Amer. Math. Soc. 29 (1993), no. 2, 151–188.CrossRefGoogle Scholar
Bergweiler, W.. On the Julia set of analytic self-maps of the punctured plane. Analysis 15 (1995), no. 3, 251–256.CrossRefGoogle Scholar
Bishop, C. J.. Constructing entire functions by quasiconformal folding. Acta Math. 214 (2015), no. 1, 1–60.CrossRefGoogle Scholar
Bergweiler, W., Rippon, P. J. and Stallard, G. M.. Multiply connected wandering domains of entire functions. Proc. Lond. Math. Soc. (3) 107 (2013), no. 6, 1261–1301.CrossRefGoogle Scholar
Bergweiler, W. and Zheng, J.-H.. Some examples of Baker domains. Nonlinearity 25 (2012), no. 4, 1033–1044.CrossRefGoogle Scholar
Cowen, C. C.. Iteration and the solution of functional equations for functions analytic in the unit disk. Trans. Amer. Math. Soc. 265 (1981), no. 1, 69–95.CrossRefGoogle Scholar
Eremenko, A. E. and Lyubich, M. Yu.. Dynamical properties of some classes of entire functions. Ann. Inst. Fourier (Grenoble) 42 (1992), no. 4, 989–1020.CrossRefGoogle Scholar
Eremenko, A. E.. On the iteration of entire functions. Dynamical systems and ergodic theory (Warsaw, 1986), Banach Center Publ., vol. 23. (PWN, Warsaw, 1989), pp. 339–345.CrossRefGoogle Scholar
Fagella, N.. Dynamics of the complex standard family. J. Math. Anal. Appl. 229 (1999), no. 1, 1–31.CrossRefGoogle Scholar
Fatou, P.. Sur l'itération des fonctions transcendantes entières. Acta Math. 47 (1926), no. 4, 337–370.CrossRefGoogle Scholar
Fagella, N. and Henriksen, C.. Deformation of entire functions with Baker domains. Discrete Contin. Dyn. Syst. 15 (2006), no. 2, 379–394.CrossRefGoogle Scholar
Fagella, N. and Martí-Pete, D.. Dynamic rays of bounded-type transcendental self-maps of the punctured plane. Discrete Contin. Dyn. Syst. 37 (2017), 3123–3160.CrossRefGoogle Scholar
Gaier, D.. Lectures on Complex Approximation (Birkhäuser Boston, Inc., Boston, MA, 1987), Translated from the German by Renate McLaughlin.Google Scholar
Gauthier, P. M., Approximating the Riemann zeta-function by strongly recurrent functions. Blaschke products and their applications. Fields Inst. Commun., vol. 65 (Springer, New York, 2013), pp. 31–42.CrossRefGoogle Scholar
Keen, L. and Lakic, N.. Forward Iterated Function Systems. Complex dynamics and related topics: lectures from the Morningside Center of Mathematics. New Stud. Adv. Math., vol. 5 (Int. Press, Somerville, MA, 2003), pp. 292–299.Google Scholar
König, H.. Conformal conjugacies in Baker domains. J. London Math. Soc. (2) 59 (1999), no. 1, 153–170.CrossRefGoogle Scholar
Kotus, J.. The domains of normality of holomorphic self-maps of C*. Ann. Acad. Sci. Fenn. Ser. A I Math. 15 (1990), no. 2, 329–340.CrossRefGoogle Scholar
Martí-Pete, D.. UEscaping points and semiconjugation of holomorphic self-maps of the punctured plane, in preparation.Google Scholar
Martí-Pete, D.. Structural theorems for holomorphic self-maps of the punctured plane. PhD. thesis. The Open University (2016).Google Scholar
Martí-Pete, D.. The escaping set of transcendental self-maps of the punctured plane. Ergod. Dynam. Sys. 38 (2018), no. 2, 739–760.CrossRefGoogle Scholar
Milnor, J. W.. Dynamics in One Complex Variable, third ed. Ann. Math. Stud. vol. 160 (Princeton University Press, Princeton, 2006).Google Scholar
Mukhamedshin, A. N.. Mapping of a punctured plane with wandering domains. Sibirsk. Mat. Zh. 32 (1991), no. 2, 184–187, 214.Google Scholar
Nersesyan, A. A.. Carleman sets. Izv. Akad. Nauk Armjan. SSR Ser. Mat. 6 (1971), no. 6, 465–471.Google Scholar
Rådström, H.. On the iteration of analytic functions. Math. Scand. 1 (1953), 85–92.CrossRefGoogle Scholar
Rippon, P. J.. Baker domains. Transcendental Dynamics and Complex Analysis, London Math. Soc. Lecture Note Ser., vol. 348 (Cambridge University Press, Cambridge, 2008), pp. 371–395.Google Scholar
Rippon, P. J. and Stallard, G. M.. On multiply connected wandering domains of meromorphic functions. J. Lond. Math. Soc. (2) 77 (2008), no. 2, 405–423.CrossRefGoogle Scholar