Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T14:52:17.814Z Has data issue: false hasContentIssue false
  • English
  • Français

Equidimensional immersions of locally compact groups

Published online by Cambridge University Press:  24 October 2008

K. H. Hofmann ,
T. S. Wu  and
J. S. Yang
K. H. Hofmann
Affiliation:
Fachbereich Mathematik, Technische Hochschule Darmstadt, Schlossgartenstr. 7, D–6100 Darmstadt, WestGermany
T. S. Wu
Affiliation:
Department of Mathematics, Case Western Reserve University, Cleveland, Ohio 44106, U.S.A.
J. S. Yang
Affiliation:
Department of Mathematics, University of South Carolina, Columbia, South Carolina 29208, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Dense immersions occur frequently in Lie group theory. Suppose that exp: g → G denotes the exponential function of a Lie group and a is a Lie subalgebra of g. Then there is a unique Lie group ALie with exponential function exp:a → ALie and an immersion f:ALie→G whose induced morphism L(j) on the Lie algebra level is the inclusion a → g and which has as image an analytic subgroup A of G. The group Ā is a connected Lie group in which A is normal and dense and the corestriction

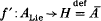
is a dense immersion. Unless A is closed, in which case f' is an isomorphism of Lie groups, dim a = dim ALie is strictly smaller than dim h = dim H.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 2 , March 1989 , pp. 253 - 261
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bourbaki, N.. Groupes et algébres de Lie, Chapitres I-IX (Hermann, 1971).Google Scholar
[2]Iwasawa, K.. On some types of topological groups. Ann. of Math. 50 (1949), 507–558.CrossRefGoogle Scholar
[3]Lashof, R.. Lie algebras of locally compact groups. Pac. J. Math. 7 (1957), 1145–1162.CrossRefGoogle Scholar