In this paper we obtain results on equicontinuity and apply them to certain recursive properties of topological transformation groups (X, T, π) with uniform phase space X. For example, in the special case that each transition πt is uniformly continuous we consider the transformation group (X,Ψ,ρ), where Ψ is the closure of {πt|t∈T} in the space of all unimorphisms of X onto X with the topology of uniform convergence (space index topology) and p(x, φ) = φ(x) for (x, φ)∈ X × Ψ. (See (1), page 94, 11·18.) If π is a mapping on X × T we usually write ‘xt’ for ‘π(x, t)’ and ‘AT’ for ‘π(A × T)’ where A ⊂ X. In this case we obtain the following results:

I. If (X, T, π) is almost periodic [regularly almost periodic] and πxis equicontinuous, then (X,Φ,ρ) is almost periodic [regularly almost periodic]

II. Let A be a compact subset of X such that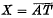. If the left and right uniformities of T are equal and (X, T, π) is almost periodic [regularly almost periodic], then (X, T, π) is almost periodic [regularly almost periodic].