Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T13:12:21.054Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding theorems for tree-free groups

Published online by Cambridge University Press:  05 May 2010

IAN CHISWELL  and
THOMAS MÜLLER
IAN CHISWELL
Affiliation:
School of Mathematical Sciences, Queen Mary & Westfield College, University of London, Mile End Road, London E1 4NS, UK.
THOMAS MÜLLER
Affiliation:
School of Mathematical Sciences, Queen Mary & Westfield College, University of London, Mile End Road, London E1 4NS, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish two embedding theorems for tree-free groups. The first result embeds a group G acting freely and without inversions on a Λ-tree X into a group 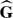acting freely, without inversions, and transitively on a Λ-tree 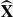in such a way that X embeds into 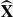by means of a G-equivariant isometry. The second result embeds a group G acting freely and transitively on an ℝ-tree X into 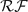(H) for some suitable group H, again in such a way that X embeds G-equivariantly into the ℝ-tree XH associated with 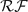(H). The group 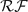(H) referred to here belongs to a class of groups introduced and studied by the present authors in [3]. As a consequence of these two theorems, we find that 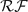-groups and their associated ℝ-trees are in fact universal for free ℝ-tree actions. Moreover, our first embedding theorem throws light on the question, arising from the results of [7], whether a group endowed with a Lyndon length function L can always be embedded in a length-preserving way into a group with a regular Lyndon length function; modulo an obvious necessary restriction we show that this is indeed the case if L is free.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 149 , Issue 1 , July 2010 , pp. 127 - 146
Copyright
Copyright © Cambridge Philosophical Society 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Alperin, R. C. and Moss, K. N.Complete trees for groups with a real-valued length function. J. London Math. Soc. 31 (1985), 55–68.CrossRefGoogle Scholar
[2]Chiswell, I. M.Introduction to Λ-Trees. (World Scientific, 2001).CrossRefGoogle Scholar
[3]Chiswell, I. M. and Müller, T. W.A Class of Groups Universal for Free ℝ-Tree Actions. (Submitted to Cambridge University Press).Google Scholar
[4]Cohn, P. M.Algebra (second edition), Volume 3. (John Wiley & Sons, 1991).Google Scholar
[5]Holt, D. F., Eick, B. and O'Brien, E.Handbook of Computational Group Theory. Discrete Mathematics and its Applications (Boca Raton) (Chapman & Hall/CRC, Boca Raton, 2005), (Birkhäuser, Basel und Stuttgart, 1975).Google Scholar
[6]Mayer, J. C., Nikiel, J. and Oversteegen, L. G.Universal spaces for ℝ-trees. Trans. Amer. Math. Soc. 334 (1992), 411–432.Google Scholar
[7]Myasnikov, A. G., Remeslennikov, V. N. and Serbin, D.Regular free length functions on Lyndon's free ℤ[t]-group F ℤ[t]. Groups, Languages, Algorithms (ed. A. V. Borovik), Contemp. Math. 378 (2005), 33–77.Google Scholar
[8]Morgan, J. W. and Shalen, P. B.Valuations, trees, and degenerations of hyperbolic structures, I. Ann. of Math. 120 (1984), 401–476.CrossRefGoogle Scholar
[9]Morgan, J. W. and Shalen, P. B.Free actions of surface groups on ℝ-trees. Topology 30 (1991), 143–154.CrossRefGoogle Scholar
[10]Newman, M. H. A.On theories with a combinatorial definition of “equivalence”. Ann. Math. 43 (1942), 223–243.CrossRefGoogle Scholar
[11]Stallings, J. R.Adian groups and pregroups. Essays in Group Theory (ed. S. M. Gersten). Math. Sci. Res. Inst. Publ. 8 (1987), 321–342.Google Scholar