Eigenvalues of smooth kernels
Published online by Cambridge University Press: 24 October 2008
Extract
Suppose 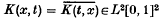 is a symmetric square integrable kernel on the unit square [0, 1]2. Then
is a symmetric square integrable kernel on the unit square [0, 1]2. Then
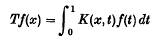
is a compact symmetric operator on the Hilbert space L2[0, 1]. H. Weyl (see [2]) has shown that, if 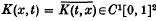 then the eigenvalues
then the eigenvalues
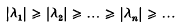
of T satisfy  as n → ∞. We prove a related result. Let W12[0, 1]2 denote the space of all K(x, t) ε L2[0, 1]2 which are absolutely continuous in x for each t and absolutely continuous in t for each x, and the partial derivatives ∂K/∂x(x, t), ∂K/∂t(x, t) are both in L2[0, 1]2. We slow that the eigenvalues of any
as n → ∞. We prove a related result. Let W12[0, 1]2 denote the space of all K(x, t) ε L2[0, 1]2 which are absolutely continuous in x for each t and absolutely continuous in t for each x, and the partial derivatives ∂K/∂x(x, t), ∂K/∂t(x, t) are both in L2[0, 1]2. We slow that the eigenvalues of any 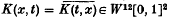 satisfy
satisfy 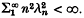 .
.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 95 , Issue 1 , January 1984 , pp. 135 - 140
- Copyright
- Copyright © Cambridge Philosophical Society 1984
References
REFERENCES
- 8
- Cited by


