Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-10T20:50:30.805Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective results for unit points on curves over finitely generated domains

Published online by Cambridge University Press:  13 January 2015

ATTILA BÉRCZES
ATTILA BÉRCZES*
Affiliation:
Institute of Mathematics, University of Debrecen, H-4010 Debrecen, P.O. Box 12, Hungary. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A be a commutative domain of characteristic 0 which is finitely generated over ℤ as a ℤ-algebra. Denote by A* the unit group of A and by K the algebraic closure of the quotient field K of A. We shall prove effective finiteness results for the elements of the set

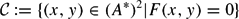\begin{equation*} \mathcal{C}:=\{ (x,y)\in (A^*)^2 | F(x,y)=0 \} \end{equation*}
where F(X, Y) is a non-constant polynomial with coefficients in A which is not divisible over K by any polynomial of the form XmYn - α or Xm - α Yn, with m, n ∈ ℤ⩾0, max(m, n) > 0, α ∈ K*. This result is a common generalisation of effective results of Evertse and Győry [12] on S-unit equations over finitely generated domains, of Bombieri and Gubler [5] on the equation F(x, y) = 0 over S-units of number fields, and it is an effective version of Lang's general but ineffective theorem [20] on this equation over finitely generated domains. The conditions that A is finitely generated and F is not divisible by any polynomial of the above type are essentially necessary.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 158 , Issue 2 , March 2015 , pp. 331 - 353
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aschenbrenner, M.Ideal membership in polynomial rings over the integers. J. Amer. Math. Soc. 17 (2004), 407–442.CrossRefGoogle Scholar
[2]Bérczes, A., Evertse, J.-H. and Győry, K.Effective results for hyper- and superelliptic equations over number fields. Publ. Math. Debrecen 82 (2013), 727–756.Google Scholar
[3]Bérczes, A., Evertse, J.-H. and Győry, K.Effective results for Diophantine equations over finitely generated domains. Acta Arith. 163 (2014), 71–100.Google Scholar
[4]Bérczes, A., Evertse, J.-H., Győry, K. and Pontreau, C.Effective results for points on certain subvarieties of tori, Math. Proc. Camb. Phil. Soc. 147 (2009), 69–94.Google Scholar
[5]Bombieri, E. and Gubler, W., Heights in Diophantine Geometry (Cambridge University Press, Cambridge, 2006).Google Scholar
[6]Brindza, B.On the equation f(x) = ym over finitely generated domains. Acta Math. Hungar. 53 (1989), 377–383.Google Scholar
[7]Brindza, B.The Catalan equation over finitely generated integral domains. Publ. Math. Debrecen 42 (1993), 193–198.Google Scholar
[8]Brindza, B. and Pintér, Á.On equal values of binary forms over finitely generated fields. Publ. Math. Debrecen 46 (1995), 339–347.CrossRefGoogle Scholar
[9]Brindza, B., Pintér, A. and Végső, J.The Schinzel–Tijdeman equation over function fields. C.R. Math. Rep. Acad. Sci. Canada 16 (1994), 53–57.Google Scholar
[10]Brownawell, W. D. and Masser, D. W.Vanishing sums in function fields. Math. Proc. Camb. Phil. Soc. 100 (1986), 427–434.Google Scholar
[11]Bugeaud, Y. and Győry, K.Bounds for the solutions of unit equations. Acta Arith. 74 (1996), 67–80.Google Scholar
[12]Evertse, J.-H. and Győry, K.Effective results for unit equations over finitely generated integral domains. Math. Proc. Camb. Phil. Soc. 154 (2013), 351–380.Google Scholar
[13]Győry, K.Sur les polynômes à coefficients entiers et de dicriminant donné II. Publ. Math. Debrecen 21 (1974), 125–144.CrossRefGoogle Scholar
[14]Győry, K.On the number of solutions of linear equations in units of an algebraic number field. Comment. Math. Helv. 54 (1979), 583–600.Google Scholar
[15]Győry, K.Bounds for the solutions of norm form, discriminant form and index form equations in finitely generated integral domains. Acta Math. Hungar. 42 (1983), 45–80.Google Scholar
[16]Győry, K.Effective finiteness theorems for polynomials with given discriminant and integral elements with given discriminant over finitely generated domains. J. Reine Angew. Math. 346 (1984), 54–100.Google Scholar
[17]Győry, K. and Yu, K.Bounds for the solutions of S-unit equations and decomposable form equations. Acta Arith. 123 (2006), 9–41.CrossRefGoogle Scholar
[18]Hermann, G.Die Frage der endlich vielen Schritte in der Theorie der Polynomideale. Math. Ann. 95 (1926), 736–788.Google Scholar
[19]Hindry, M. and Silverman, J. H.Diophantine Geometry. Graduate Texts in Mathematics, vol. 201 (Springer-Verlag, New York, 2000).Google Scholar
[20]Lang, S. Integral points on curves. Inst. Hautes Études Sci. Publ. Math. (1960), 27–43.Google Scholar
[21]Louboutin, S.Explicit bounds for residues of Dedekind zeta functions, values of L-functions at s = 1, and relative class numbers. J. Number Theory 85 (2000), 263–282.Google Scholar
[22]Mahler, K.Zur Approximation algebraischer Zahlen. I. Math. Ann. 107 (1933), 691–730.Google Scholar
[23]Parry, C. J.The p-adic generalisation of the Thue–Siegel theorem. Acta Math. 83 (1950), 1–100.Google Scholar
[24]Siegel, C.Approximation algebraischer Zahlen. Math. Z. 10 (1921), 173–213.Google Scholar